Olá, pessoal!
Meu código atual já realiza todos os passos do exercício, mas gostaria de receber sugestões de como posso melhorar a lógica do cálculo ou a visualização, especialmente para:
Tornar o código mais limpo ou compacto.
Melhorar a interpretação visual das retas e das médias.
Obs: Eu segui a lógica da equação, calculando os desvios em relação à média passo a passo, pois achei mais intuitivo. Contudo, na prática, acredito que não seja a maneira mais eficiente, como o próprio código do instruto mostra. Gostaria de saber se alguém teria dicas para manter essa clareza pedagógica, mas ao mesmo tempo deixar o código mais enxuto ou os gráficos mais elegantes.
import matplotlib.gridspec as gridspec
import matplotlib.pyplot as plt
import numpy as np
# --- Carregando os dados ---
url_2 = 'https://raw.githubusercontent.com/YuriArduino/Estudos_Numpy/refs/heads/Datas_tests/citrus.csv'
fruit_data = np.loadtxt(url_2, delimiter=',', skiprows=1, usecols=np.arange(1,6))
# --- Separando as frutas ---
# Laranjas
orange_diameters = fruit_data[:5000, 0] # diâmetros
orange_weights = fruit_data[:5000, 1] # pesos
# Toranjas
grapefruit_diameters = fruit_data[5000:, 0]
grapefruit_weights = fruit_data[5000:, 1]
# --- Calculando médias ---
x_mean = np.mean(orange_diameters) # média dos diâmetros laranja
y_mean = np.mean(orange_weights) # média dos pesos laranja
z_mean = np.mean(grapefruit_diameters) # média dos diâmetros toranja
w_mean = np.mean(grapefruit_weights) # média dos pesos toranja
# --- Cálculo da reta de regressão (laranjas) ---
desvios_diametro_laranja = orange_diameters - x_mean # x_i - média dos diâmetros
desvios_peso_laranja = orange_weights - y_mean # y_i - média dos pesos
numerador_laranja = np.sum(desvios_diametro_laranja * desvios_peso_laranja) # Σ(x_i - x̄)(y_i - ȳ)
denominador_laranja = np.sum(desvios_diametro_laranja**2) # Σ(x_i - x̄)^2
m_laranja = numerador_laranja / denominador_laranja # coeficiente angular: inclinação da reta
b_laranja = y_mean - m_laranja * x_mean # coeficiente linear: ponto onde a reta cruza o eixo y
# --- Cálculo da reta de regressão (toranjas) ---
desvios_diametro_toranja = grapefruit_diameters - z_mean # x_i - média dos diâmetros
desvios_peso_toranja = grapefruit_weights - w_mean # y_i - média dos pesos
numerador_toranja = np.sum(desvios_diametro_toranja * desvios_peso_toranja) # Σ(x_i - x̄)(y_i - ȳ)
denominador_toranja = np.sum(desvios_diametro_toranja**2) # Σ(x_i - x̄)^2
m_toranja = numerador_toranja / denominador_toranja # coeficiente angular
b_toranja = w_mean - m_toranja * z_mean # coeficiente linear
# --- Preparando a figura com 3 gráficos ---
fig = plt.figure(figsize=(12,12))
gs = gridspec.GridSpec(3, 1, height_ratios=[2, 1, 1], hspace=0.4)
# --- Gráfico principal (ambas as frutas) ---
ax0 = fig.add_subplot(gs[0])
ax0.scatter(orange_diameters, orange_weights, color='orange', label='Laranja', alpha=0.3, s=30)
ax0.scatter(grapefruit_diameters, grapefruit_weights, color='purple', label='Toranja', alpha=0.3, s=30)
ax0.scatter(x_mean, y_mean, color='red', marker='x', s=100, label='Média Laranja')
ax0.scatter(z_mean, w_mean, color='blue', marker='x', s=100, label='Média Toranja')
# Retas de regressão
x_range_laranja = np.linspace(min(orange_diameters), max(orange_diameters), 100)
y_range_laranja = m_laranja * x_range_laranja + b_laranja
ax0.plot(x_range_laranja, y_range_laranja, color='orange', linewidth=2, label='Reta Laranja')
x_range_toranja = np.linspace(min(grapefruit_diameters), max(grapefruit_diameters), 100)
y_range_toranja = m_toranja * x_range_toranja + b_toranja
ax0.plot(x_range_toranja, y_range_toranja, color='purple', linewidth=2, label='Reta Toranja')
ax0.set_xlabel('Diâmetro')
ax0.set_ylabel('Peso')
ax0.set_title('Comparativo: Diâmetro e Peso com Retas de Regressão')
ax0.legend()
ax0.grid(True)
# --- Gráfico só laranjas ---
ax1 = fig.add_subplot(gs[1])
ax1.scatter(orange_diameters, orange_weights, color='orange', alpha=0.3, s=20)
ax1.scatter(x_mean, y_mean, color='red', marker='x', s=100, label='Média Laranja')
ax1.plot(x_range_laranja, y_range_laranja, color='orange', linewidth=2)
ax1.set_xlabel('Diâmetro')
ax1.set_ylabel('Peso')
ax1.set_title('Somente Laranjas')
ax1.grid(True)
# --- Gráfico só toranjas ---
ax2 = fig.add_subplot(gs[2])
ax2.scatter(grapefruit_diameters, grapefruit_weights, color='purple', alpha=0.3, s=20)
ax2.scatter(z_mean, w_mean, color='blue', marker='x', s=100, label='Média Toranja')
ax2.plot(x_range_toranja, y_range_toranja, color='purple', linewidth=2)
ax2.set_xlabel('Diâmetro')
ax2.set_ylabel('Peso')
ax2.set_title('Somente Toranjas')
ax2.grid(True)
plt.show()






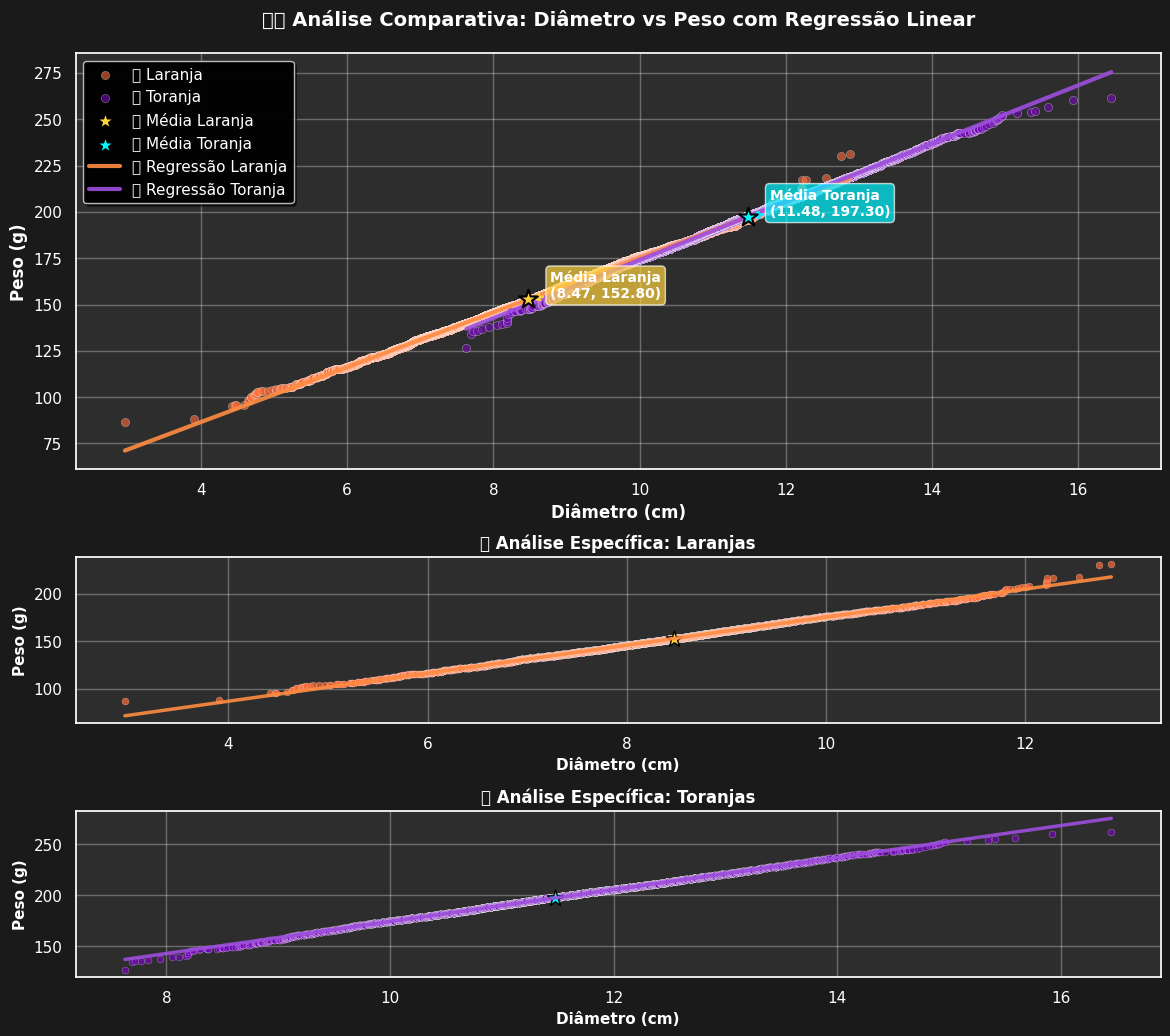 )
)