Desafio: gráficos de distribuição de dados para duas variáveis numéricas e/ou categóricas

Desafio 1

import pandas as pd

notas = pd.read_csv('https://raw.githubusercontent.com/Gabriellemga/Python_Cursos_Alura/refs/heads/main/Data_viz_graficos_distribui%C3%A7%C3%A3o_compara%C3%A7%C3%A3o/dados/notas.csv')
notas.sample(7)

import matplotlib.pyplot as plt
import seaborn as sns

fig , ax =  plt.subplots(figsize = (10,5))
sns.set_theme(style = 'whitegrid')

ax = sns.violinplot(data = notas, x = 'Turma', y = 'Nota', palette = [AZUL2, VERDE1, AMARELO1])

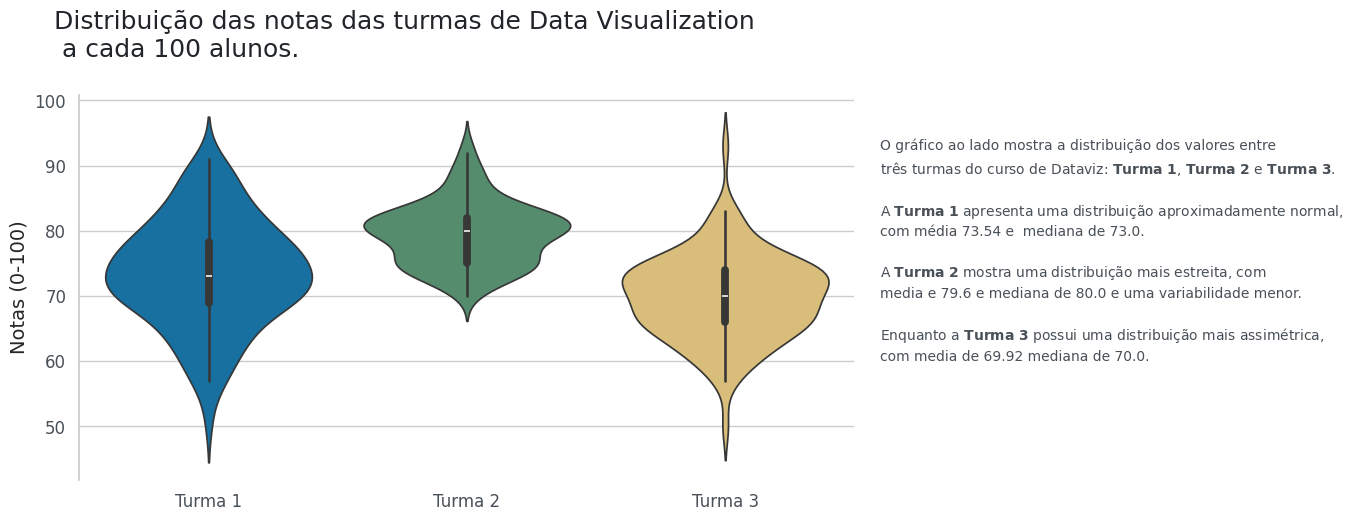
plt.suptitle('Distribuição das notas das turmas de Data Visualization\n a cada 100 alunos.', size=18, color=CINZA1, ha = 'left', x = 0.1, y = 1.05)
ax.set_xlabel('')
ax.set_ylabel('Notas (0-100)', fontsize = 14)
ax.xaxis.set_tick_params(labelsize=12, labelcolor = CINZA2)
ax.yaxis.set_tick_params(labelsize=12, labelcolor = CINZA2)
sns.despine(bottom=True)

mediana = []
media = []
for i in range(1,4):
  mediana.append(notas.query(f"Turma == 'Turma {i}'").Nota.median())
  media.append(notas.query(f"Turma == 'Turma {i}'").Nota.mean())  


ax.text(2.6, 60,
         'O gráfico ao lado mostra a distribuição dos valores entre\n'
         'três turmas do curso de Dataviz: $\\bf{Turma\ 1}$, $\\bf{Turma\ 2}$ e $\\bf{Turma\ 3}$.\n\n'
         'A $\\bf{Turma\ 1}$ apresenta uma distribuição aproximadamente normal,\n'
         f'com média {media[0]} e  mediana de {mediana[0]}.\n\n'
         'A $\\bf{Turma\ 2}$ mostra uma distribuição mais estreita, com\n' 
         f'media e {media[1]} e mediana de {mediana[1]} e uma variabilidade menor.\n\n'
         'Enquanto a $\\bf{Turma\ 3}$ possui uma distribuição mais assimétrica,\n'
         f'com media de {media[2]} mediana de {mediana[2]}.',
         fontsize=10, linespacing=1.45, color=CINZA2)

plt.show()

Desafio 2

df_medidas = pd.read_csv("https://raw.githubusercontent.com/alura-cursos/dataviz-graficos/master/dados/medidas_sabao_em_po.csv")
df_medidas.sample(5)

medidas_b = df_medidas.query("amostra == 'B'")[['comprimento', 'largura']]
medidas_b

import matplotlib.pyplot as plt 
import seaborn as sns
import numpy as np

fig , ax = plt.subplots(figsize = (10,5))
sns.set_theme(style = 'white')

cores = [VERMELHO1, LARANJA1, AZUL2]
pct = 0.02
rejeita_larg = [True if (a > 5*(1+pct) or a < 5*(1-pct)) else False for a in medidas_b["largura"]]
map_cores = np.where(rejeita_larg, cores[0], np.where(rejeita_larg, cores[1], cores[2]))

ax = sns.scatterplot(data = medidas_b, x = 'comprimento', y = 'largura', color = map_cores)

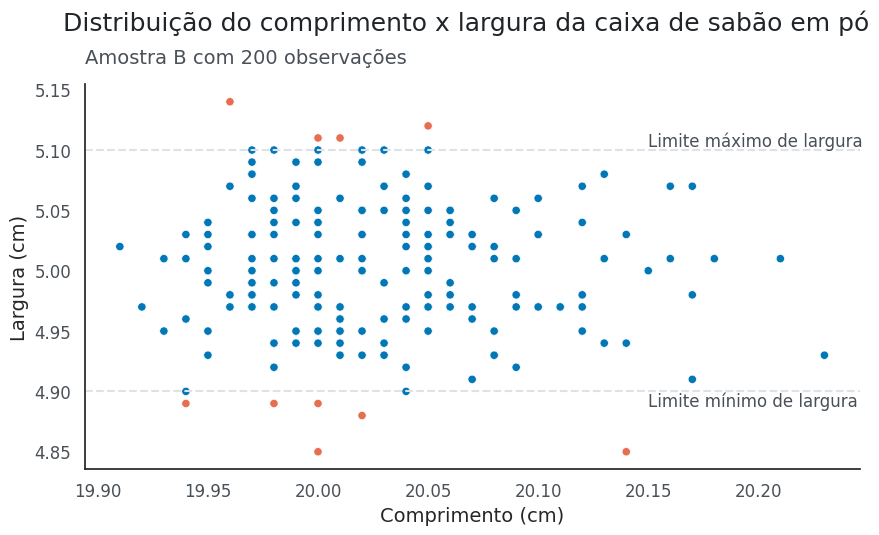
plt.suptitle('Distribuição do comprimento x largura da caixa de sabão em pó', size=18, color=CINZA1, ha = 'right', x = 0.91, y = 1.03)
plt.title('Amostra B com 200 observações', fontsize=14, color=CINZA2, pad = 15, loc = "left")
ax.set_xlabel('Comprimento (cm)',  fontsize = 14)
ax.set_ylabel('Largura (cm)', fontsize = 14)
ax.xaxis.set_tick_params(labelsize=12, labelcolor = CINZA2)
ax.yaxis.set_tick_params(labelsize=12, labelcolor = CINZA2)
sns.despine()

ax.text(20.15, 5.1, 'Limite máximo de largura', fontsize=12, color = CINZA2, ha="left", va = "bottom")
plt.axhline(y = 5 * (1 + pct), color = CINZA4, linestyle='--')
ax.text(20.15, 4.9, 'Limite mínimo de largura', fontsize=12, color = CINZA2, ha="left", va = "top")
plt.axhline(y = 5 * (1 - pct), color = CINZA4, linestyle='--')

plt.show()