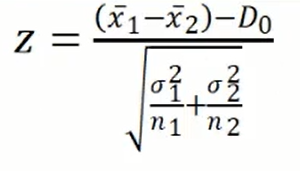No video que o professor exemplifica o teste para duas amostras com o dataset dos rendimento dos chefes de domicílio, para verificar a igualdade das médias entre homens e mulheres. Neste caso, para poder aplicar esse teste não deveria pressupor que as populações se distribuem como uma distribuição normal? Só que o teste de normalidade aplicado na amostra, diz que os dados não se distribuem como uma normal.
Solucionado (ver solução)
Solucionado
(ver solução)
2
respostas
respostas
Teste para duas amostras - Populações que se distribuem como uma normal
solução!
Olá Paulo, tudo bem? Espero que sim!
Desculpe pela demora em retornar.
Um teste paramétrico pressupõe a normalidade para a estatística de teste e não para a distribuição dos dados. No teste adotado da aula, a estatística de teste é dada por:
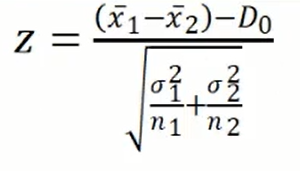
Temos que, conforme o aumento do tamanho das amostras, as distribuições das estatísticas de teste irão satisfazer as condições do teste, você pode checar isso através do teorema do limite central. O tamanho das amostras no exemplo da aula são grandes, com n1 = n2 = 500. Isso é suficiente para que possa ser utilizado o teste paramétrico.
No geral, os testes paramétricos tem mais poder do que os testes não paramétricos e esse é um motivo pelo qual ele já seria mais indicado, mas isso pode se inverter caso você tenha amostras muito pequenas, nesse caso, os testes não paramétricos podem ser melhores. Mas tudo irá depender também do que você estará testando.
Vou deixar aqui dois links que falam um pouco dessa questão de uso de testes paramétricos e não paramétricos:
O primeiro conteúdo se encontra em inglês
- T teste para dados não normais quando n>50
- Como escolher entre um teste não paramétrico e um teste paramétrico
Espero que tenha tirado sua dúvida.
Estou à disposição. Bons estudos!
Caso este post tenha lhe ajudado, por favor, marcar como solucionado ✓. Bons Estudos!
Obrigado pelo retorno