Oi. Não entendi como o professor transformou o b = (1200 - a²) / 4a na seguinte expressão: V(a) = a²[(300/a) - (a/4)]. Pq substituindo o b a expressão se torna [(300/a) - (a/4)]?
Obrigado
Oi. Não entendi como o professor transformou o b = (1200 - a²) / 4a na seguinte expressão: V(a) = a²[(300/a) - (a/4)]. Pq substituindo o b a expressão se torna [(300/a) - (a/4)]?
Obrigado
Olá Rafael, tudo bem? Espero que sim!
Vou deixar uma explicação completa do problema, mas você pode descer até a simplificação da expressão caso queira.
Considerando que a seja o valor do lado da base e b seja a altura da caixa, podemos construir duas expressões, uma para o volume e outra para a área total com exceção do topo:
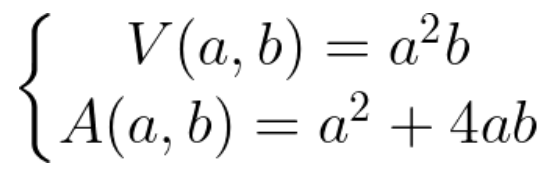
O volume V(a,b) foi encontrado obtendo a área da base quadrada a*a multiplicado pela altura b.
O cálculo da área total, que não possui tampa é a área da base quadrada a*a acrescido da área de cada uma das faces da caixa, que possuem comprimento a e altura b, portanto a*b é a área de uma face, como a caixa possui 4 faces desse tamanho, obtemos 4*a*b. Se possuísse tampa, a área da tampa seria a mesma área da base, tornando a equação 2a²+4ab.
A área total foi dada com valor 1200 cm². Portanto podemos substituir na expressão da área:
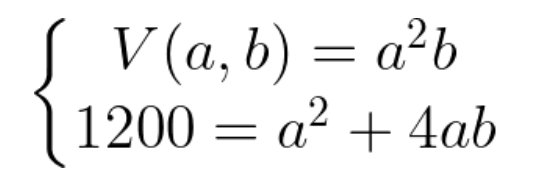
Vamos isolar o termo b na expressão da área para realizar uma substituição do valor na expressão do Volume V(a,b).
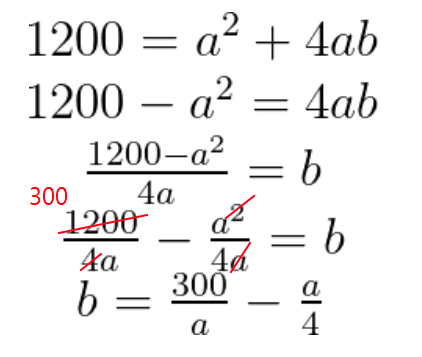
Observe que o 1200 foi dividido por 4 e o a² foi dividido por a, simplificando a expressão e retornando o valor de b.
Com isso, podemos substituir na expressão do volume:
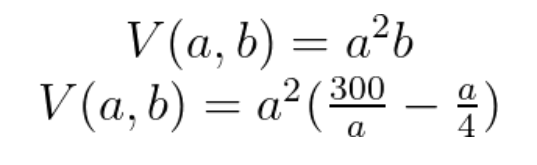
Espero que tenha tirado sua dúvida.
Estou à disposição. Bons estudos!