1. Calcule o desvio padrão amostral das avaliações.
import numpy as np
dp_amostra = np.std(df_techtaste.values, ddof=1)
print("desvio padrão amostral:",dp_amostra)
2. Calcule o erro padrão amostral da média para as avaliações dos clientes.
calculo do valor critico (Zalpha/2)
# calculo do valor critico (Zalpha/2)
from scipy.stats import norm
nivel_de_confianca = 0.9
alpha = 1 - nivel_de_confianca
z_alpha_2 = norm.ppf(1 - alpha/2)
print(f"Valor crítico para nivel de confiança de {nivel_de_confianca * 100:.2f}%:", z_alpha_2)
erro_padrao_amostral_mu = z_alpha_2 * (dp_amostra/np.sqrt(len(df_techtaste)))
print("Erro Padrão Amostral da média:", erro_padrao_amostral_mu)
3. Utilizando um gráfico de histograma, analise visualmente a distribuição das avaliações dos clientes.
import matplotlib.pyplot as plt
plt.hist(df_techtaste, bins=15, color="darkblue")
plt.show()
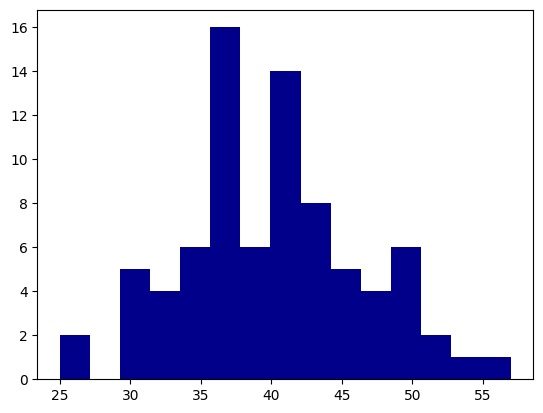
4. Observe o formato da distribuição gerado no histograma. Ele se assemelha a uma distribuição normal?
Sim. Se assemelha no formato. No entanto, não parece ser simétrica. E sim, assimétrica à direita.
5. Com um nível de confiança de 90%, calcule o intervalo de confiança para a média das avaliações.
li_IC = np.mean(df_techtaste) + erro_padrao_amostral_mu
ls_IC = np.mean(df_techtaste) - erro_padrao_amostral_mu
print(f"IC (90%): [{round(ls_IC, 5)}; {round(li_IC, 5)}]")
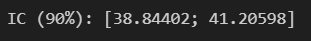
6. A largura do intervalo de confiança seria afetada se o nível de confiança fosse aumentado para 95%?
Sim. Ficaria um intervalo mais estreito
nível de confinça de 90%]
nivel_de_confianca_90 = 0.90
alpha = (1 - nivel_de_confianca_90)/2
z_alpha_2 = norm.ppf(1 - alpha/2)
print(f"Valor crítico para nivel de confiança de {nivel_de_confianca_90 * 100:.2f}%:", z_alpha_2)
# nivel de confiança de 95%
nivel_de_confianca_95 = 0.95
alpha = (1 - nivel_de_confianca_95)/2
z_alpha_2 = norm.ppf(1 - alpha/2)
print(f"Valor crítico para nivel de confiança de {nivel_de_confianca_95 * 100:.2f}%:", z_alpha_2)
Conte com o apoio da comunidade Alura na sua jornada. Abraços e bons estudos!