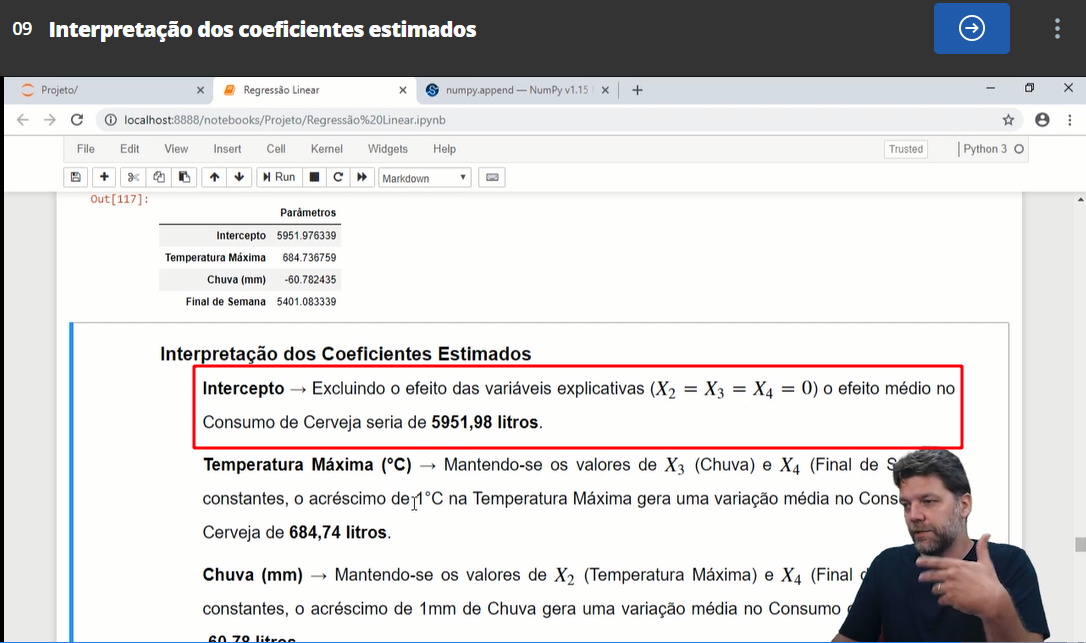
Há um erro nesta questão e no vídeo correspondente.
O intercepto da equação de regressão não o resultado estimado excluindo todas as variáveis explicativas.
Excluir uma variável do modelo é não rodar o modelo com ela.
Se você apenas posiciona a variável explicativa em zero para calcular sua estimativa, você está apenas está fazendo uma predição na origem.
No próprio exemplo dado pelo professor, de predizer um consumo de cerveja com base na temperatura e outras variáveis:
Se você estimar o consumo de cerveja com temperatura zero, você não estará excluindo o efeito da temperatura do modelo. Apenas está estimando qual será o consumo de cerveja a zero grau.