[Dúvida] Resultado do melhor caminho na solução sugerida

Olá, Caina!

Muito obrigado pela sua pergunta. É uma excelente observação, e mostra que você está pensando de forma crítica sobre a aplicação do algoritmo, o que é fundamental para um bom engenheiro de software.

Para o algoritmo A*, o melhor caminho não é necessariamente o de menor custo total no final, mas sim aquele que, a cada iteração, tem a menor soma de f(n) = g(n) + h(n), onde:

• g(n) é o custo real do caminho do ponto de partida até o nó atual.

• h(n) é o custo estimado (a heurística) do nó atual até o destino.

Você está correto ao dizer que em um primeiro momento o caminho A -> B pode parecer mais vantajoso, mas é preciso analisar todos os passos da expansão do A*.

O algoritmo A* explora os nós com base na menor f(n). Se a soma dos custos (g(n) e h(n)) do caminho A -> B -> C for menor do que a do caminho A -> C em algum momento da exploração, o A* vai seguir por esse caminho. Pode ser que o custo real (g(n)) de A -> B seja pequeno, e a heurística (h(n)) de B -> C também seja baixa, fazendo com que a soma f(n) do caminho A -> B seja mais atrativa inicialmente, e ele continue por ali.

Se a solução apresentada no curso está em conflito com o seu entendimento, pode haver três motivos:

1. A heurística (h(n)) não é admissível: Uma heurística admissível nunca superestima o custo real até o objetivo. Se a heurística usada no curso superestimou o custo de A -> C em algum ponto, o A* pode ter sido levado a escolher um caminho não ideal.

2. A implementação do A possui um erro:* É possível que o código tenha alguma falha.

3. A minha interpretação do problema está incorreta: Precisaria rever os valores de g(n) e h(n) para cada passo do algoritmo para confirmar qual caminho realmente seria o de menor custo.

O seu raciocínio está correto, e é o cerne do funcionamento do A*. A melhor forma de tirar a dúvida é refazendo a simulação do algoritmo passo a passo, calculando f(n) para cada nó expandido, para ver se os valores da solução do curso se sustentam. Se você puder compartilhar os valores de g(n) e h(n) usados no exemplo do instrutor, eu posso te ajudar a verificar.

@Caina também fritei a cabeça com essa resposta, mas pelo que entendi estamos com uma cabeça maio "dijkstra" para solução, na real achei que aula ficou BEEEEM vaga sobre o assunto e não teve aprofundamento necesssário para que possamos entender.

Vou mesclar o que entendi com o Gemini + NotebookLM para e ai podemos ver se fui na linha correta.

O A* combina duas coisas:

• o custo real para se mover entre os nós
• e a heurística (com o valor que atribuimos a cada nó)

Ele não escolhe um caminho apenas pela heurística. Ele usa a seguinte fórmula para decidir: f(n) = g(n) + h(n) que está lá no comentário do código. O g(n) é o custo real do caminho desde o nó inicial (Produto A) até o nó atual (n), no código, cada "passo" entre um produto e outro tem um custo de 1 (pois não temos peso atribuído na aresta). O h(n) é a heurística, tipo o que ele vai pensar, ou seja, uma estimativa de custo do nó atual (n) até o objetivo (Produto C). No código, a heurística proposta é baseada na probabilidade de conversão. O algoritmo A* sempre vai explorar o nó que tiver o menor valor de f(n)

Ai simuland o algoritmo començando no produto A o algoritmo avalia os caminhos possíveis: ir para Prduto B ou ir direto para Produto C.

Para ir ao nó B:                                                                                                                                                                                                                  
* g(B) = 1 (custo real para sair de A e chegar em B, valor da aresta)                
* h(B) = 8 (heurística do nó B, obs: tirei o decimal)                                                                                                                                                                                             
* f(B) = 1 + 8 = 9

Para ir ao nó C (direto):                 
* g(C) = 1 (custo real para sair de A e chegar em C)          
* h(C) = 7 (heurística do nó C)   
* f(C) = 1 + 7 = 8

Neste cenário hipotético, o algoritmo escolheria o caminho A -> C porque f(C) é 8, que é menor que f(B) que é 9. Mas lembra que a função heuristica faz uma "negativação dos valores" que faz com que escolha f(B) e ai por fim ir para f(C). Na A* tem essa heuristica que meio que funciona como uma "bússola", dando ao algoritmo uma noção de direção.

---
config:
  layout: fixed
---
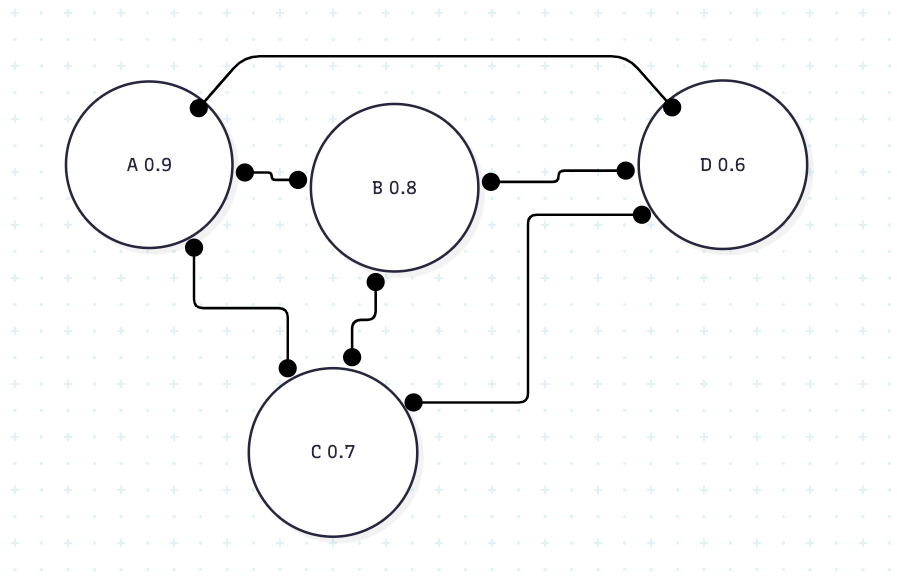
flowchart LR
    a(("A 0.9")) o--o b(("B 0.8")) & c(("C 0.7")) & d(("D 0.6"))
    b o--o c & d
    c o--o d