[Dúvida] Detecção de outliers: IQR vs Z-score vs Regra dos 3 sigmas

Olá, pessoal.

Compartilho abaixo minha solução para o Desafio: identificando fraudes, comparando três métodos de detecção de outliers demonstrados na seção "Para saber mais: formas de identificar outliers":

1. IQR (Interquartile Range)
2. Z-score
3. Regra dos 3 sigmas

1. Preparando os dados

import pandas as pd
import numpy as np
import seaborn as sns

# Dados simulados
df = pd.DataFrame({
    'ID da transação': range(1, 31),
    'Valor da transação': [
        100, 200, 150, 500, 300, 913, 250, 400, 200, 150,
        200, 200, 400, 300, 150, 301, 805, 300, 400, 250,
        150, 100, 500, 600, 200, 350, 100, 250, 800, 250
    ],
    'Data da transação': pd.date_range(start='2022-01-01', periods=30, freq='D'),
    'Local da transação': ['São Paulo, Brasil'] * 27
                           + ['Nova Iorque, EUA', 'Los Angeles, EUA', 'Miami, EUA']
})

Visualização rápida (boxplot):

sns.boxplot(x=df['Valor da transação']);

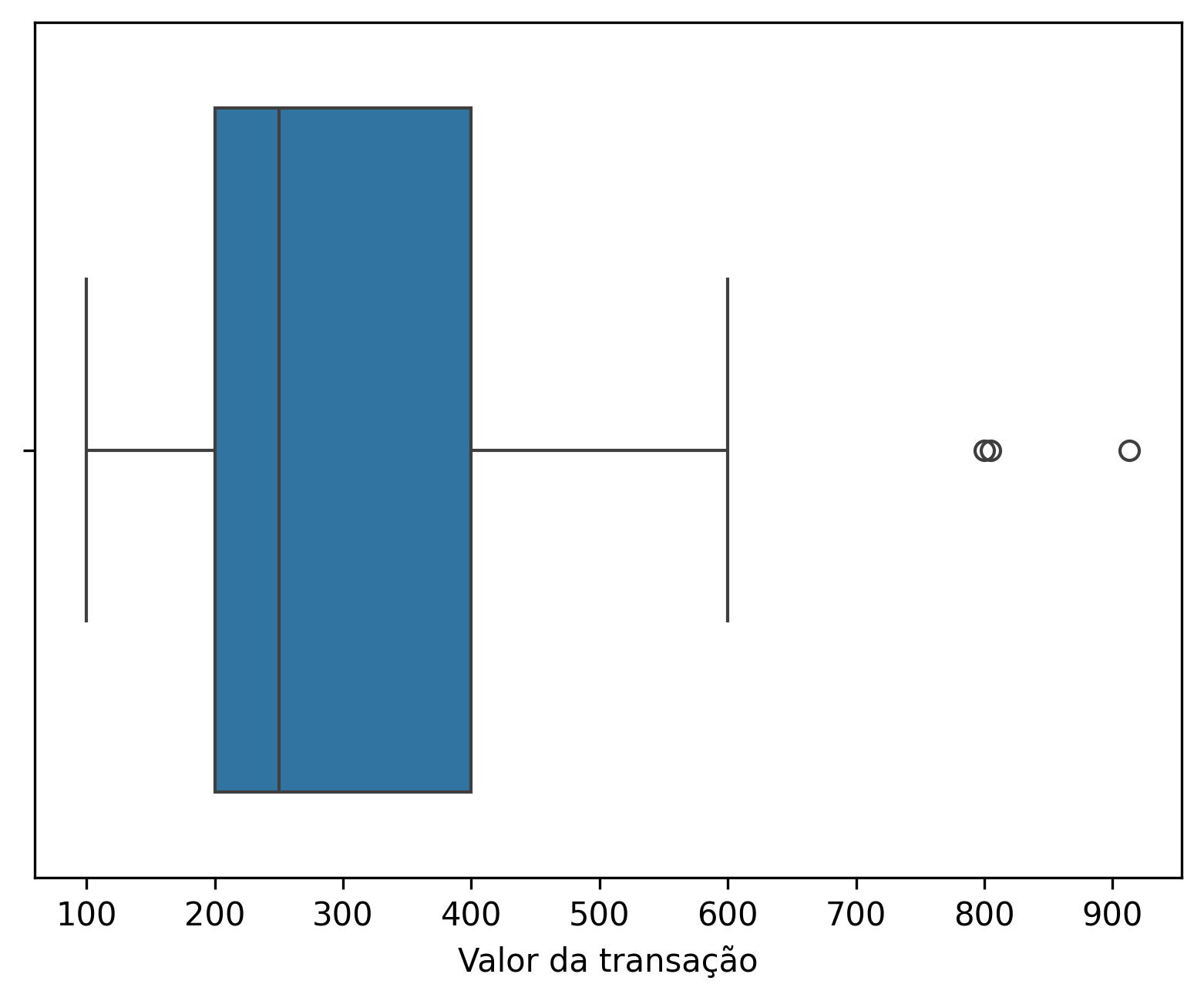
2. Detecção por IQR

def detecta_outliers_iqr(df: pd.DataFrame, coluna: str) -> pd.DataFrame:
    """
    Retorna as linhas em que o valor da coluna está fora
    de [Q1 - 1.5·IQR, Q3 + 1.5·IQR].
    """
    Q1 = df[coluna].quantile(0.25)
    Q3 = df[coluna].quantile(0.75)
    IQR = Q3 - Q1

    lim_inf = Q1 - 1.5 * IQR
    lim_sup = Q3 + 1.5 * IQR

    mascara = (df[coluna] < lim_inf) | (df[coluna] > lim_sup)
    return df[mascara]

Teste:

outliers_iqr = detecta_outliers_iqr(df, 'Valor da transação')
print(outliers_iqr[['ID da transação', 'Valor da transação']])

Saída (IQR):

   ID da transação  Valor da transação
5                6                 913
16              17                 805
28              29                 800

3. Detecção por Z-score

def detecta_outliers_zscore(
    df: pd.DataFrame,
    coluna: str,
    limite: float = 3.0
) -> pd.DataFrame:
    """
    Retorna as linhas com |Z-score| > limite.
    Z-score = (x - média) / desvio_padrão (populacional).
    """
    valores = df[coluna]
    z_scores = (valores - valores.mean()) / valores.std(ddof=0)
    mascara = np.abs(z_scores) > limite
    return df[mascara]

Teste com limite padrão (3.0):

outliers_z1 = detecta_outliers_zscore(df, 'Valor da transação', limite=3.0)
print("Outliers (Z-score, lim=3.0):", outliers_z1[['ID da transação', 'Valor da transação']])

Teste ajustando para 2.2 (para comparar com IQR):

outliers_z2 = detecta_outliers_zscore(df, 'Valor da transação', limite=2.2)
print("Outliers (Z-score, lim=2.2):", outliers_z2[['ID da transação', 'Valor da transação']])

Saída (Z-score, lim=2.2):

   ID da transação  Valor da transação
5                6                 913
16              17                 805
28              29                 800

4. Detecção pela Regra dos 3 sigmas

def detecta_outliers_sigma(
    df: pd.DataFrame,
    coluna: str,
    n_sigmas: float = 3.0
) -> pd.DataFrame:
    """
    Retorna as linhas em que o valor da coluna está fora
    de [média - n_sigmas·σ, média + n_sigmas·σ].
    """
    valores = df[coluna]
    media = valores.mean()
    sigma = valores.std(ddof=0)

    lim_inf = media - n_sigmas * sigma
    lim_sup = media + n_sigmas * sigma

    mascara = (valores < lim_inf) | (valores > lim_sup)
    return df[mascara]

Teste com 3 sigmas:

outliers_s3 = detecta_outliers_sigma(df, 'Valor da transação', n_sigmas=3.0)
print("Outliers (3 sigmas):", outliers_s3[['ID da transação', 'Valor da transação']])

Teste ajustando para 2.2 sigmas:

outliers_s22 = detecta_outliers_sigma(df, 'Valor da transação', n_sigmas=2.2)
print("Outliers (2.2 sigmas):", outliers_s22[['ID da transação', 'Valor da transação']])

Saída (2.2 sigmas):

   ID da transação  Valor da transação
5                6                 913
16              17                 805
28              29                 800

5. Conclusões e Pergunta

• IQR detectou automaticamente os 3 valores mais extremos sem ajustes.
• Z-score e Regra dos 3 sigmas exigiram reduzir o limite de 3 para 2.2 para encontrar exatamente os mesmos outliers.

Pergunta: Existe um "padrão ouro" ou guia prático para escolher qual método e quais parâmetros usar em diferentes cenários?

Abraço!