Olá Lucas, tudo bem? Espero que sim!

Desculpe pela demora em retornar.

A fórmula EQM foi apresentada na Aula 01- Atividade 04: Passos Iniciais. Essa fórmula representa o erro quadrático médio, ou seja, a média da diferença entre o valor previsto e o valor real elevados ao quadrado. O erro quadrático médio é dado pela equação:

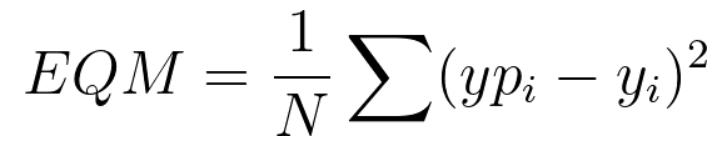
Na Aula 03 - Atividade 02: O método do gradiente descendente foram apresentadas as fórmulas das derivadas parciais de EQM em relação ao θ0 e θ1, portanto elas derivam diretamente da função EQM acima. Vamos realizar a derivada de EQM em relação a θ0 e depois em relação a θ1:

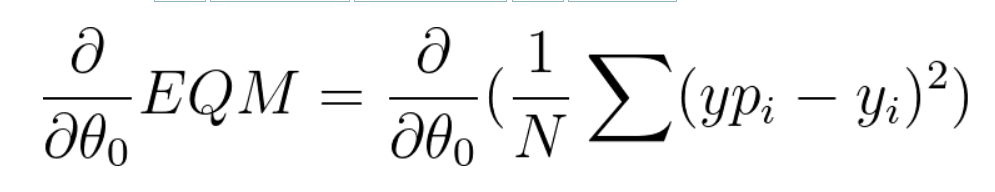
A derivada da expressão à direita em relação a θ0 será resolvida utilizando a regra da cadeia, visto que há uma função quadrática na expressão (yp_i - y_i)². O valor que depende de θ0 é o y previsto, dada pela expressão:

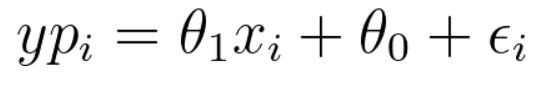
Portanto, pela regra da cadeia, teremos o produto da derivada da função quadrática vezes a derivada da expressão interna. O valor 2 do expoente multiplicará a expressão total, e devemos fazer a derivada da expressão yp_i. Como a derivada é em relação a θ0, teremos que a derivada da expressão é igual a 1, uma vez que θ1*x_i e ε_i não dependem de θ0 e têm derivada igual a 0.

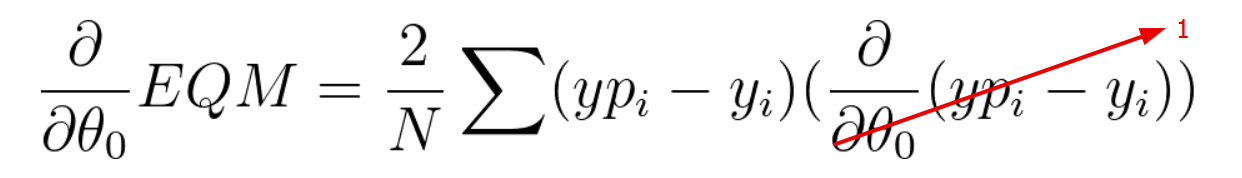
Resultando na expressão da derivada parcial em relação a θ0 dada na aula. A derivada parcial em relação a θ1 se difere somente na derivada da expressão yp_i - y_i. Como θ1 está multiplicado por x_i na expressão de yp_i, temos que a derivada parcial é igual a x_i. Logo:

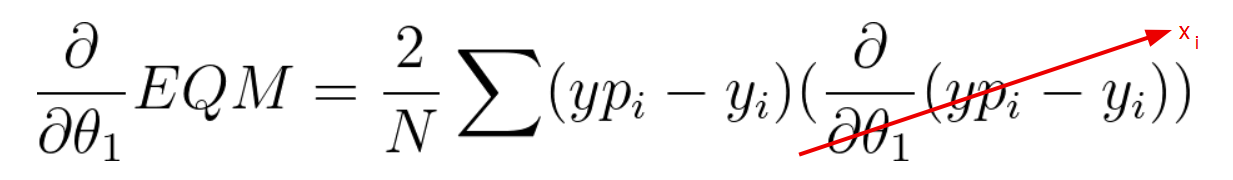
Espero que tenha tirado sua dúvida.

Estou à disposição. Bons estudos!