A distância entre os usuários, afinal. O número que dá, ele é soma dos valores conseguidos pelo Pitágoras? A distância com dois pontos deu pra entender, mas quando temos n pontos? o que faz a função np.linalg.norm() ? Que cálculo ela faz?
A distância entre os usuários, afinal. O número que dá, ele é soma dos valores conseguidos pelo Pitágoras? A distância com dois pontos deu pra entender, mas quando temos n pontos? o que faz a função np.linalg.norm() ? Que cálculo ela faz?
Ola,
Bom, a resposta de como calcular a distância entre n* pontos vem lá da geometria analítica e da álgebra linear. Ambas partem de uma definição de pontos e depois avançam para os espaços vetoriais (não vou entrar em detalhe aqui do que é um espaço vetorial*) basicamente é um sistema de referência, cujo os elementos podem ser pontos, vetores, ou outras coisas.
Por exemplo,
o plano cartesiano é formado pelos pares ordenados (a,b) , tal que os valores a, b são reais.
Note que os pares ordenados (a,b) constituem um ponto do plano cartesiano, o ponto A = (1,2) pertence ao plano cartesiano.
Agora vamos a definição de vetor nesse plano cartesiano. O vetor também será um par ordenado (a,b) mas com algumas propriedades adicionais, como a direção, a soma de dois vetores e o chamado módulo ou norma que é definida como a distância do ponto (a,b) até o ponto (0,0). (Note que a função do numpy é np.linalg.norm(), linalg vem de linear algebra e o norm vem de norma).
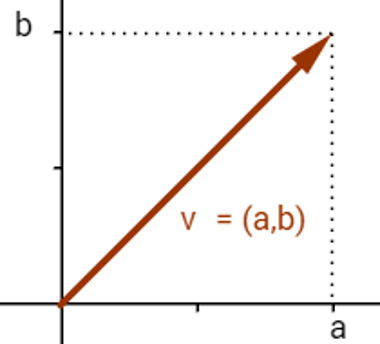
Note que a direção do vetor é dada sempre saindo do ponto (0,0) e indo até (a,b). Além disso, do teorema de Pitágoras sabemos como calcular a hipotenusa deste triangulo retângulo
|V|² = (a - 0)² + (b - 0)² → |V| = √(a² + b²)
e esta é a norma do vetor v = (a,b).
Agora em vez de trabalhar com o plano cartesiano, vamos imaginar um espaço cartesiano, compostos pelas mesmas regras anteriores, mas com uma dimensão a mais:
o espaço cartesiano é formado pelos n-conjutos ordenados (a,b,c) , tal que os valores a, b e c são reais.
Para definir os vetores neste espaço cartesiano fazemos a mesma coisa que fizemos no plano, " O vetor v será o conjunto ordenado (a,b,c) que tem uma propriedade chamada módulo, que é a distância de (a,b,c) ao ponto (0,0,0)" .

Note que a soma de todos os vetores cinzas resulta no vetor preto. Ou seja, calculando a soma do vetor ax + ay vai resultar num vetor no plano (xy) que tem um módulo dado pelo teorema de pitagoras. Quando somamos o vetor em (xy) com o vetor az teremos o vetor em (x,y,z) e este vetor também tem um módulo dado pelo teorema de Pitágoras.
A norma do vetor preto no espaço (x,y,z), será dada por:
|V| = √(ax² + ay² + az²)
É importante salientar que assim como fizemos o mesmo racíocinio de duas dimensões (plano XY) para o problema de três dimensões (espaço XYZ) podemos fazer o mesmo para quatro dimensões, cinco, até infinito. Infelizmente acima de 3 dimensões perdemos a representação visual e ai começa a álgebra linear. Respondendo a pergunta, é este calculo que a função np.linalg.norm()faz.
Vou deixar algumas referências aqui caso precise de mais informações:
OLIVEIRA, Ivan de Camargo; BOULOS, Paulo. Geometria analítica: um tratamento vetorial. São Paulo: MacGraw-Hill, 1986. (A segunda edição deste livro é muito boa)
BOLDRINI, José Luiz et al. Álgebra Linear, 3a edição. Sao Paulo: Editora Harbra Ltda, 1980.
Disciplina: Álgebra Linear 1, com o Prof. Dr. Claudio Possani, do IME-USP