Sempre que eu tiver que calcular z_alpha para unicaudais, devo colocar o nível de confiança direto na função norm.ppf( )?
Independente da cauda que estaremos trabalhando, é só colocar z_alpha = norm.ppf(confianca)?
Você está vendo a versão anterior da nova experiência da Alura que estamos preparando para você. Em breve, ela ganha uma identidade visual novinha totalmente pensada em potencializar seus estudos!
Solucionado
Sempre que eu tiver que calcular z_alpha para unicaudais, devo colocar o nível de confiança direto na função norm.ppf( )?
Independente da cauda que estaremos trabalhando, é só colocar z_alpha = norm.ppf(confianca)?
Olá Júlio, tudo bem? Espero que sim!
Desculpe pela demora em retornar.
Vamos entender como a função norm.ppf() funciona para que fique claro o resultado que ela retorna.
A função norm.ppf() é o inverso da função norm.cdf(), que é a função distribuição acumulada da distribuição normal.
Na imagem a seguir, podemos ver o gráfico da distribuição normal e da distribuição acumulada. A distribuição acumulada é a soma da probabilidade da distribuição normal até o ponto x em questão.
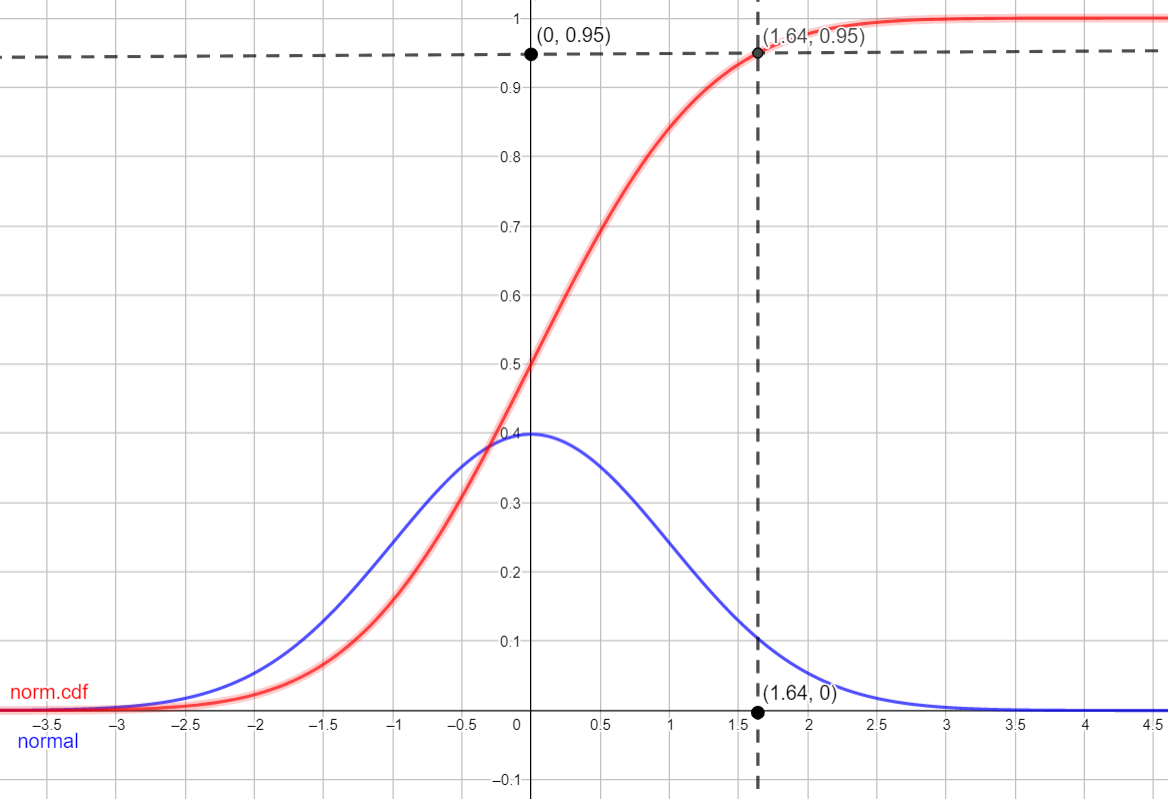
A curva em azul representa a distribuição normal, enquanto a curva em vermelho representa a função norm.cdf, ou seja, a distribuição acumulada. Na figura, também há o destaque para três pontos, o ponto (1.64, 0) no eixo das abcissas, o ponto (0, 0.95) nas ordenadas e o ponto de cruzamento entre eles ao traçar retas paralelas aos eixos y e x respectivamente. Esse ponto de encontro é o ponto (1.64, 0.95) que intercepta a curva de distribuição acumulada.
Portanto, para cada valor de x, teremos um valor na função de distribuição acumulada que corresponde à probabilidade acumulada da função normal de -∞ até esse valor x. A probabilidade acumulada da distribuição normal para um x = 1.64 equivale a 0.95 ou 95%.
Como a função norm.ppf() é o inverso da função norm.cdf, ela retornará para cada valor y de probabilidade, um valor x que corresponde ao valor Z da distribuição normal. Portanto, utilizando a função norm.ppf, para o valor 0.95 de probabilidade, obteremos o valor 1.64 que corresponde ao Z no eixo x.
Portanto, se utilizarmos o nível de confiança diretamente na função norm.ppf, obteremos um Z associado a esse nível de confiança. Os níveis de confiança mais utilizados são (0.90, 0.95 e 0.99), obtendo valores de Z (1.28, 1.64 e 2.32) respectivamente.
Esses valores são referentes ao Z-alpha para análise unicaudal à direita, já que os valores de Z-alpha para análise unicaudal à esquerda seriam os valores negativos (-1.28, -1.64 e -2.32), por isso deve-se tomar certo cuidado.
Já para análise bicaudal, teremos que utilizar outros valores, já que a probabilidade será dividida para ambos os lados da curva normal, e para os mesmos níveis de confiança (0.90, 0.95 e 0.99), teremos que utilizar os valores (0.95, 0.975 e 0.995) na função norm.ppf(), obtendo os Z-alphas (1.64, 1.96 e 2.57) e seus respectivos valores simétricos (-1.64, -1.96 e -2.57).
Espero que tenha tirado sua dúvida.
Estou à disposição. Bons estudos!