A inclinação das retas é sempre a mesma?

Olá Fabiano,

Boa pergunta.

Referente aos coeficientes angular

Sua interpretação está correta. Cada variável independente terá seu próprio valor de coeficiente, que indica a variação da variável resposta (Y) para cada acréscimo da variável de entrada (X)

Referente ao intercepto:

A medida que você altera as variáveis independentes na regressão linear simples ou que você acrescenta novas variáveis independentes na regressão múltipla, o valor do intercepto tende a mudar. Isso ocorre porque, quando o algoritmo está ajustando o modelo linear aos dados, o valor do intercepto que melhor se ajusta, depende do coeficiente angular das variáveis independentes. Veja:

# Referência número (2)
valor do intercepto = Y(bar) - coeficiente_angular * X(bar)

Logo, cada alteração que você no conjunto de variáveis independentes, você altera o valor do intercepto

Referências

1. Equação da reta

2. Parâmetros do modelo

Abs

Agradeço a dedicação na resposta, mas ainda não ficou claro pra mim.

Preciso retomar o caso do vídeo. Lá foi apresentada duas retas. Uma para cada variável independente, certo?

Por que não foi utilizado dois coeficientes angulares?

Olá Fabiano, tudo bem? Espero que sim!

Desculpe pela demora em retornar.

A fórmula para o modelo de regressão linear múltipla é a seguinte:

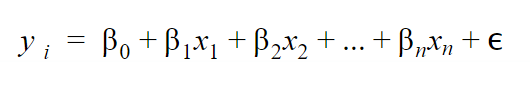
Onde y é a variável resposta que em nosso caso é a qualidade do ar (airq).

O βo é o intercepto, ou seja, o valor onde a reta passa pelo eixo y. Ele é o primeiro valor dado no summary e vale para toda reta que iremos construir.

Os outros βs são os coeficientes de cada uma das variáveis explicativas. No nosso caso, existem duas variáveis explicativas, vala que é o valor das empresas e coas que significa se a cidade é costeira ou não costeira. Os coeficientes dessas variáveis também são encontrados no summary.

Substituindo esses valores na fórmula de regressão linear múltipla, obtemos:

y = 117.1 + 0.001999 x1 - 29.68 x2

Onde x1 representa a variação em vala com valores contínuos de 0 a 20.000 e x2 representa a variável coas que pode assumir apenas os valores 0 e 1 (0 quando não é costeira e 1 quando é costeira).

Não conseguimos representar toda essa fórmula em um plano bidimensional apenas com uma reta, isso acontece porque os valores de x1 e x2 variam de forma diferente. Isso ficaria ainda mais complicado se todas as variáveis fossem contínuas (nesse caso escolheríamos um eixo de referência e alguns valores para outra variável e montaríamos retas diferentes para esses valores).

Como vala é a variável contínua, montamos um gráfico de dispersão a partir dele, variando o eixo x de 0 a 20.000. Não conseguiríamos representar uma reta colocando coas como eixo x, pois ela é uma variável qualitativa, e apresentaria apenas boxplot como uma visualização.

Portanto, como coas só apresenta 2 valores, podemos representar nosso modelo com duas fórmulas, uma quando x2 = 0 e outra quando x2 = 1.

• y = 117.1 + 0.001999 x1 - 29.68 x 0
• y = 117.1 + 0.001999 x1 - 29.68 x 1

Resultando em duas retas:

• y = 117.1 + 0.001999 x1
• y = 117.1 + 0.001999 x1 - 29.68

O modelo apresenta coasyes para entendermos quando a variável é acrescentada, ou seja, quando x2 = 1. Repare que isso faz com que somente o intercepto seja modificado, resultando em uma reta com a mesma inclinação mas deslocada para baixo.

Espero que tenha tirado sua dúvida.

Bons estudos!