Não entendi o traço extra que aparece somente entre a iv e a is
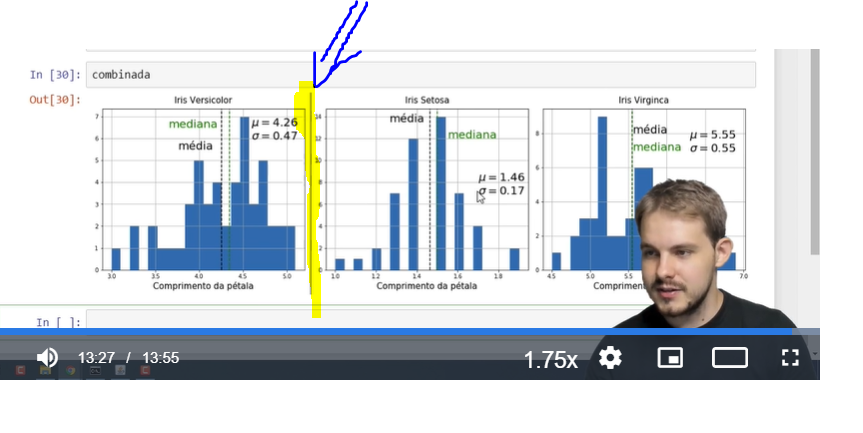
Não entendi o traço extra que aparece somente entre a iv e a is

Olá, Christian, tudo bem?
Isso é algo bem interessante, não é mesmo?
Quando realizei o curso também achei um pouco estranho e não encontrei algo no código que pudesse criar essa linha a mais na imagem. Acredito que seja um pequeno erro ocasionado na junção das imagens pelas as funções presentes no módulo Image da PIL .
Como outra abordagem para gerar essa imagem sem esse traço extra, podemos usar a função subplots da própria biblioteca da matplolib (plt). Vou deixar logo aqui abaixo o trecho do código que poderá auxiliá-lo nessa construção. Fique atento aos nomes das variáveis e escolhas que realizei dos nomes das variáveis para que possa reproduzir em seu código.
# Usando subplot para desenhar 3 gráficos numa mesma figura e salvando com savefig
# Aqui a variável 'fig' corresponde a figura inteira e o 'ax' cada um dos gráficos que iremos plotar
# Temos 1 linha e 3 colunas como a orientação que queremos desenhar nossos gráficos
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(18,5))
# Gráfico 01 - Iris Versicolor
df_iv = df[df['espécie'] == 'Iris-versicolor']
mu, sigma = df_iv['comprimento_pétala'].mean(), df_iv['comprimento_pétala'].std()
# ax[0] - Define o 1º gráfico e todas as alterações pertencentes a ele
ax[0].hist(df_iv['comprimento_pétala'], bins = 20)
ax[0].set_title('Histograma Iris Versicolor', fontsize = 15, pad = 10)
ax[0].set_xlabel('Comprimento da pétala', fontsize = 15)
ax[0].grid(True)
ax[0].annotate('$\mu = {0:.2f}$\n$\sigma={1:.2f}$'.format(mu, sigma),
xy=(4.6, 6), fontsize=20)
ax[0].axvline(df_iv['comprimento_pétala'].mean(), color='k', linestyle='--')
ax[0].annotate('média', xy=(df_iv['comprimento_pétala'].mean()-0.5, 5.5), fontsize=20)
ax[0].axvline(df_iv['comprimento_pétala'].median(), color='g', linestyle='--')
ax[0].annotate('mediana', xy=(df_iv['comprimento_pétala'].median() - 0.7, 6.5), fontsize=20, color = 'g')
# Gráfico 02 - Íris Setosa
df_is = df[df['espécie'] == 'Iris-setosa']
mu, sigma = df_is['comprimento_pétala'].mean(), df_is['comprimento_pétala'].std()
# ax[1] - Define o 2º gráfico e todas as alterações pertencentes a ele
ax[1].hist(df_is['comprimento_pétala'], bins = 20)
ax[1].set_title('Histograma Iris Setosa', fontsize = 15, pad = 10)
ax[1].set_xlabel('Comprimento da pétala', fontsize = 15)
ax[1].grid(True)
ax[1].annotate('$\mu = {0:.2f}$\n$\sigma={1:.2f}$'.format(mu, sigma),
xy=(1.7, 7), fontsize=20)
ax[1].axvline(df_is['comprimento_pétala'].mean(), color='k', linestyle='--')
ax[1].annotate('média', xy=(df_is['comprimento_pétala'].mean()-0.2, 13.5), fontsize=20)
ax[1].axvline(df_is['comprimento_pétala'].median(), color='g', linestyle='--')
ax[1].annotate('mediana', xy=(df_is['comprimento_pétala'].median()+0.05, 12), fontsize=20, color = 'g')
# Gráfico 03 - Íris Virgínica
df_ivg = df[df['espécie'] == 'Iris-virginica']
mu, sigma = df_ivg['comprimento_pétala'].mean(), df_ivg['comprimento_pétala'].std()
# ax[2] - Define o 1º gráfico e todas as alterações pertencentes a ele
ax[2].hist(df_ivg['comprimento_pétala'], bins = 20)
ax[2].set_title('Histograma Iris Virgínica', fontsize = 15, pad = 10)
ax[2].set_xlabel('Comprimento da pétala', fontsize = 15)
ax[2].grid(True)
ax[2].annotate('$\mu = {0:.2f}$\n$\sigma={1:.2f}$'.format(mu, sigma),
xy=(6.3, 7), fontsize=20)
ax[2].axvline(df_ivg['comprimento_pétala'].mean(), color='k', linestyle='--')
ax[2].annotate('média', xy=(df_ivg['comprimento_pétala'].mean(), 8), fontsize=20)
ax[2].axvline(df_ivg['comprimento_pétala'].median(), color='g', linestyle='--')
ax[2].annotate('mediana', xy=(df_ivg['comprimento_pétala'].median(), 7), fontsize=20, color = 'g')
# Salvando a figura
fig.savefig('histogramas.png', bbox_inches='tight')
plt.show()Espero ter ajudado e qualquer dúvida é só chamar!
Forte abraço!