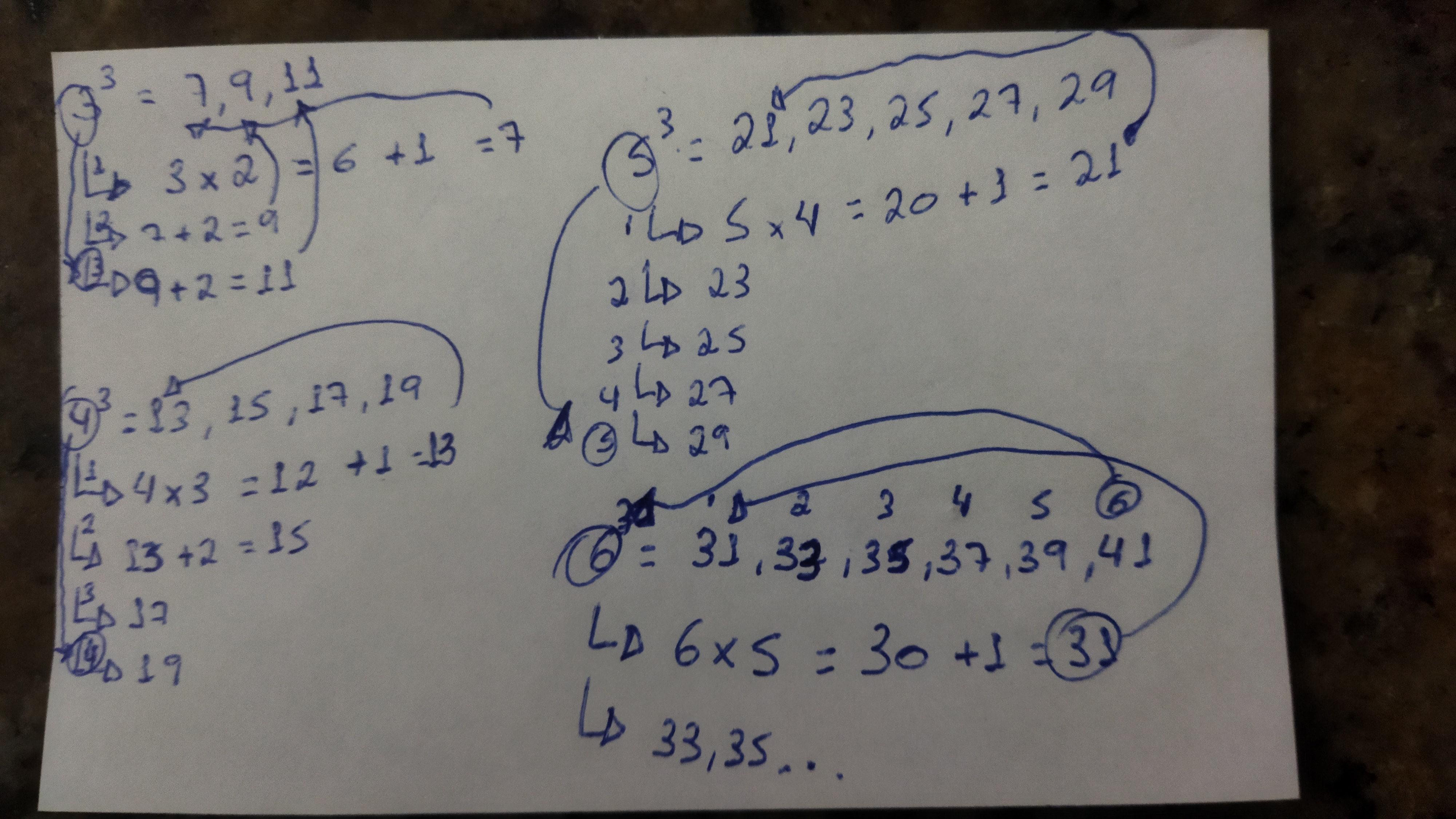Em qual tema especificamente você está com dúvidas? Na lógica do exercício, no calculo, nos resultados, nos padrões... ?
A propósito, no seu último tópico você não marcou uma resposta como "solução", resolveu o problema? Da uma conferida lá
Tirei um tempo aqui pra anotar o exercício e através dos 4 exemplos dados, peguei um papel e anotei para encontrar padrões.
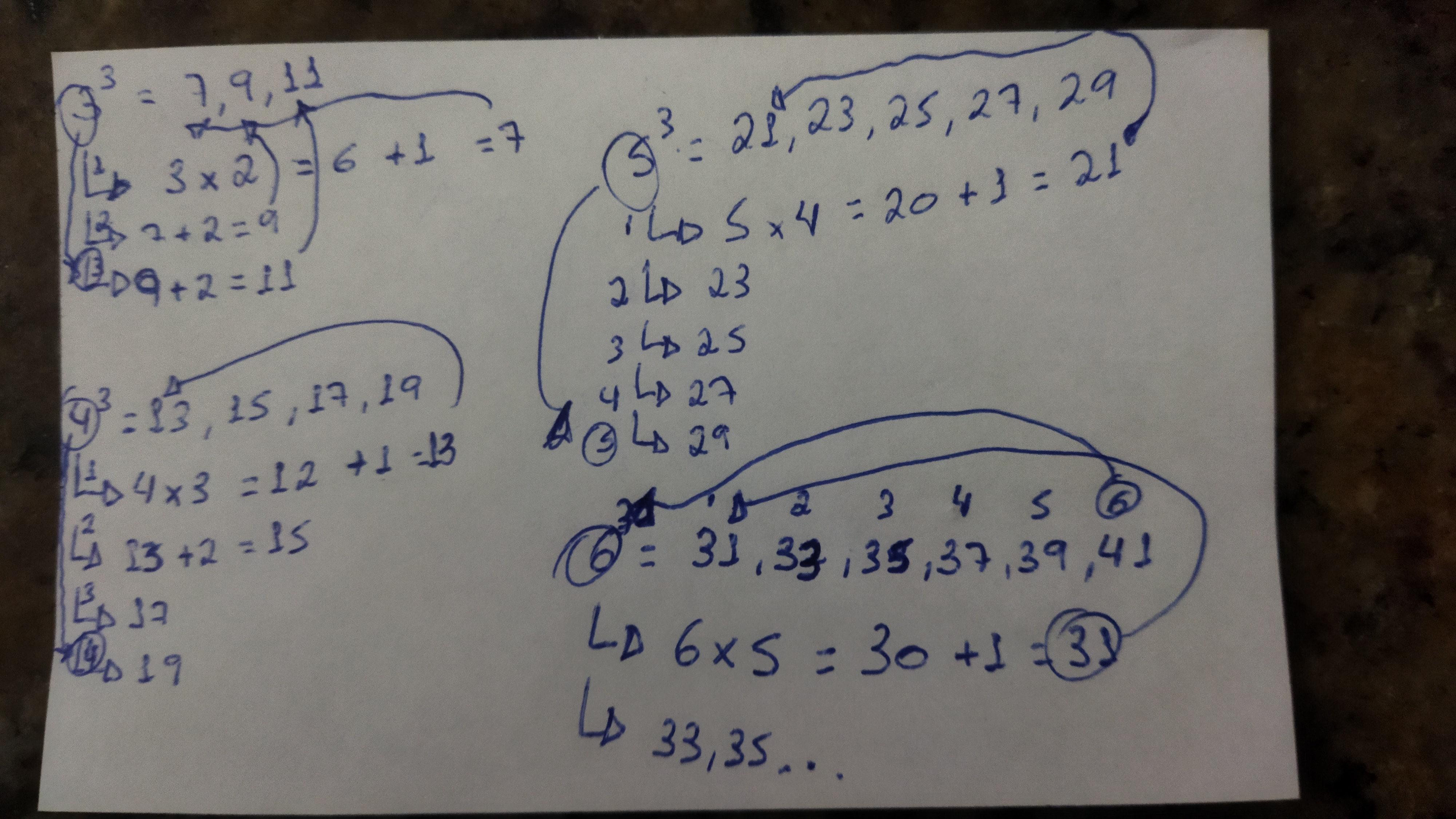
Pelas anotações eu notei que o único número que precisa de um cálculo seria o primeiro da lista, pois os demais bastaria somar 2 para obter. A quantidade de somas necessárias também já nos foi fornecida, que é M.
Ex: 3³ = (7, 9, 11) = 27 | 4³ = (13, 15, 17, 19) = 64 | 5³ = (21, 23, 25, 27, 29) = 125...
Note acima, o nosso M determina quantos números ímpares há entre nossos parênteses. Por agora já sabemos qual é nosso M e quantos números ímpares precisamos na lista para somar todos eles e no final dar o resultado certo de M ao cubo. Então agora o que falta? Como eu disse acima, precisamos saber como obter o primeiro número da lista.
Sem alongar muito, eu notei que se multiplicarmos M por M - 1, teremos um número PAR antes do correto, por exemplo, vou lhe demonstrar essa analogia utilizando os 3 exemplos acima:
- 3 x 2 = 6 (mas o correto seria 7)
- 4x3 = 12 (mas o correto seria 13)
- 5x4 = 20 (mas o correto seria 21)
Aqui encontramos mais um padrão útil, se todos números que obtemos nesses cálculos nós "erramos" o resultado por 1, então basta somar 1 ao resultado e resolvemos o problema.
Pronto, agora temos tudo o que precisamos: sabemos o valor de M, sabemos como encontrar o primeiro número, sabemos quantos números ímpares são necessários para obter o resultado correto do cálculo, então bora pro código:
m = int(input("Digite o valor de m: ")) #Recebe o número de M
start = m * (m-1) + 1 #Obtem o primeiro número da ordem multiplicando nosso M por M - 1 e somamos 1 ao resultado
list_numbers = [start] #Cria uma lista e adiciona o primeiro número na lista
for n in range(1, m): #cria um loop para adicionar os demais números ímpares restantes
start += 2 #cada soma de 2 sob um número impar sempre dará impar
list_numbers.append(start) #adiciona o próximo número ímpar na lista
print(list_numbers) #mostra a lista na tela
Agora deixo pra você fazer as implementações restantes, que é mostrar na tela de forma organizada todos esses valores e seus respectivos resultados :)