Não entendi o porquê a lógica de subtrair o raio resolveria o problema da bolinha voltar do lado esquerdo para o direito, sem encostar na parte central da bolinha, caso especificamente em xBolinha - raio < 0.
Não entendi o porquê a lógica de subtrair o raio resolveria o problema da bolinha voltar do lado esquerdo para o direito, sem encostar na parte central da bolinha, caso especificamente em xBolinha - raio < 0.
Oi, Caio! Tudo bem?
Para compreendermos melhor, primeiro, devemos visualizar o plano cartesiano do p5:

A partir dele notamos que a sua extremidade superior esquerda representa a origem do plano, e ele se estende positivamente tanto no eixo x (horizontal), quanto no eixo y (vertical).
Devemos visualizar também que a localização de xBolinha é sempre dada por um ponto localizado no meio da bolinha, logo se quisermos a posição da extremidade direita da bolinha, devemos calcular xBolinha + raio, e se quisermos a posição da extremidade esquerda da bolinha, devemos calcular a xBolinha - raio. Como é possível ver na imagem abaixo:
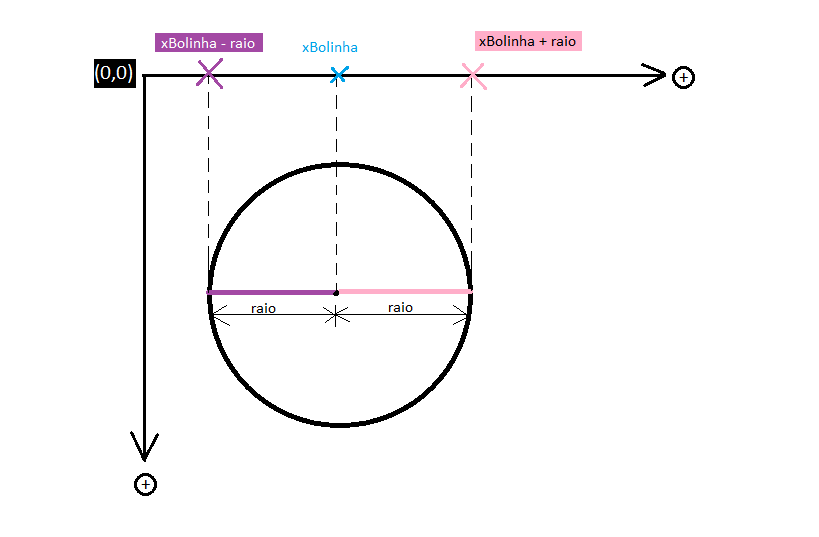
Dessa forma com o comando:
if (xBolinha + raio > width || xBolinha < 0) {
velocidadeXBolinha *= -1;
}Estamos dizendo com (xBolinha + raio > width) que a bolinha deve retornar quando a sua extremidade direita for maior que a largura do plano, ou seja, assim que a extremidade direita da bolinha tocar a borda direita do plano, ela irá retornar. Entretanto, estamos dizendo com o comando ( xBolinha < 0), que quando a localização do meio da bolinha for menor que zero, ou seja, quando o meio da bolinha atingir a extremidade esquerda do plano, ela deverá retornar.
Dessa forma, para que ao lado esquerdo do plano a bolinha não entre pela metade, mas a sua extremidade direita ao tocar a extremidade direita do plano volte, devemos acrescentar o -raio no comando, da seguinte forma:
if (xBolinha + raio > width || xBolinha - raio < 0) {
velocidadeXBolinha *= -1;
}Espero ter ajudado! Caso tenha ficado qualquer dúvida, sinta-se a vontade em comunicar!
Um forte abraço e bons estudos!