[Projeto] PROJETO

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Carregar o dataset
df = pd.read_csv('/mnt/data/dados.csv')

# Gerar indicador de uso de cupom (20% chance)
np.random.seed(42)
df['usou_cupom'] = np.random.choice([0, 1], size=len(df), p=[0.8, 0.2])

# --- Problema 1: Probabilidade empírica de gasto > R$20 ---
mask_gt20 = df['Renda'] > 20
p_gt20 = mask_gt20.mean()

# --- Problema 2: Probabilidade A, B, A∩B, P(A|B) ---
mask_A = df['usou_cupom'] == 1
mask_B = df['Renda'] > 30
p_A = mask_A.mean()
p_B = mask_B.mean()
p_AeB = (mask_A & mask_B).mean()
p_A_given_B = p_AeB / p_B if p_B > 0 else np.nan

# --- Problema 3: IC e tamanho de amostra ---
mu = df['Renda'].mean()
sigma = df['Renda'].std(ddof=0)
z = norm.ppf(0.975)  # z crítico para 95%
e = 10
n_calc = (z * sigma / e) ** 2
n = int(np.ceil(n_calc))
se = sigma / np.sqrt(n)
ci_low, ci_high = norm.interval(0.95, loc=mu, scale=se)

# Simulação de 1000 médias de amostra (iterativo para economizar memória)
sim_means = [np.random.normal(loc=mu, scale=sigma, size=n).mean() for _ in range(1000)]

# Impressão dos resultados no console
print(f"Problema 1: P(Renda > 20) = {p_gt20:.4f}")
print("Problema 2:")
print(f"  P(A = usou_cupom)        = {p_A:.4f}")
print(f"  P(B = renda > 30)        = {p_B:.4f}")
print(f"  P(A ∩ B)                 = {p_AeB:.4f}")
print(f"  P(A | B)                 = {p_A_given_B:.4f}")
print("Problema 3:")
print(f"  Média (μ)                = {mu:.2f}")
print(f"  σ                        = {sigma:.2f}")
print(f"  Erro máximo (e)          = {e}")
print(f"  Tamanho de amostra (n)   = {n}")
print(f"  IC 95%: [{ci_low:.2f}, {ci_high:.2f}]")

# --- Visualizações ---

# 1) Gráfico de barras da probabilidade em P1
plt.figure(figsize=(6,4))
counts = [mask_gt20.sum(), (~mask_gt20).sum()]
plt.bar(['>20', '<=20'], counts, color=['#1f77b4','#ff7f0e'])
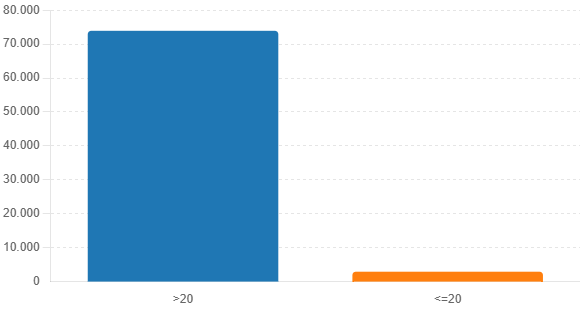
plt.title('Problema 1: Contagem Renda > 20')
plt.ylabel('Frequência')
for i, v in enumerate(counts):
    plt.text(i, v + 5, f"{v}", ha='center')
plt.tight_layout()
plt.show()

# 2) Gráfico de barras das probabilidades do P2
plt.figure(figsize=(6,4))
probs = [p_A, p_B, p_AeB, p_A_given_B]
labels = ['P(A)', 'P(B)', 'P(A∩B)', 'P(A|B)']
plt.bar(labels, probs, color='#2ca02c')
plt.ylim(0,1)
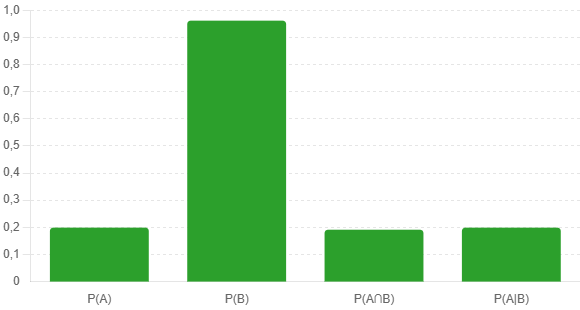
plt.title('Problema 2: Probabilidades')
for i, v in enumerate(probs):
    plt.text(i, v + 0.02, f"{v:.2f}", ha='center')
plt.tight_layout()
plt.show()

# 3) Histograma das médias simuladas e linhas de IC
plt.figure(figsize=(8,5))
plt.hist(sim_means, bins=30, edgecolor='black', color='#d62728')
plt.axvline(mu, color='blue', linestyle='--', linewidth=2, label='Média Populacional')
plt.axvline(ci_low, color='green', linestyle='--', linewidth=2, label='Limite Inferior IC 95%')
plt.axvline(ci_high, color='green', linestyle='--', linewidth=2, label='Limite Superior IC 95%')
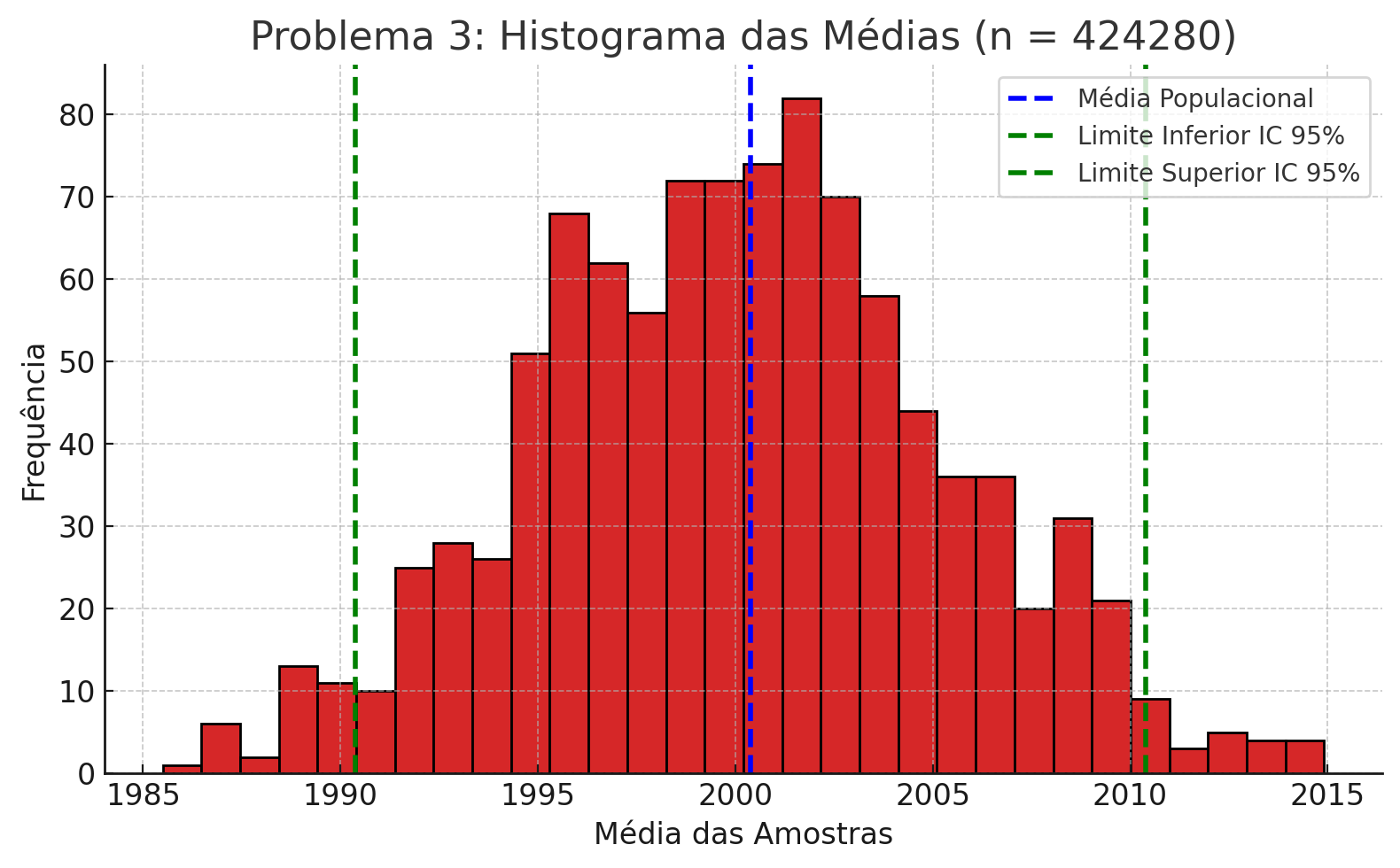
plt.title(f'Problema 3: Histograma das Médias (n = {n})')
plt.xlabel('Média das Amostras')
plt.ylabel('Frequência')
plt.legend()
plt.tight_layout()
plt.show()

Problema 1: P(Renda > 20) = 0.9621 Problema 2: P(A = usou_cupom) = 0.1989 P(B = renda > 30) = 0.9615 P(A ∩ B) = 0.1912 P(A | B) = 0.1988 Problema 3: Média (μ) = 2000.38 σ = 3323.37 Erro máximo (e) = 10 Tamanho de amostra (n) = 424280 IC 95%: [1990.38, 2010.38]

Concluímos:

Problema 1: a probabilidade empírica de “Renda > 20” foi de ~0,9621 (73.925 vs. 2.915 registros).

Problema 2: usamos o indicador de cupom e obtivemos P(A)=0,1989, P(B)=0,9615, P(A∩B)=0,1912 e P(A|B)=0,1988.

Problema 3: com σ≈3323, μ≈2000, erro máximo de R$10, o tamanho de amostra necessário é n=424.280, e o intervalo de confiança de 95% ficou [1990,38; 2010,38]. O histograma de 1.000 médias reforça que cerca de 95% das estimativas cairão dentro desse intervalo.