Boas Gabriel e Vinícius! Tudo bem? Espero que sim!
O teste de Mann-Whitney pode serr utilizado para testes bicaudais como unicaudais. O parâmetro alternative é justamente o que define se o teste é unicaucal ou bi, e no caso de ser bicaudal, qual das caudas será comparada.
Vamos revisar um pouco sobre hipóteses e testes bicaudais!
Em estatística, quando formulamos testes de hipóteses, devemos sempre nos atentar à duas questões:
- a hipótese nula (H0 é sempre o contrário de h1.
Nesse caso, podemos ter alguns tipos de hipóteses nulas e alternativas:
Testes Bicaudais:
Teste de hipótese para bicaudais
H0: μ1 = μ2
H1: μ1 ≠ μ2
Esse teste é bicaudal porque se temos um nível de significância de 95%, e então os 5% restantes vão der divididos nas caudas inferiores e superiores:
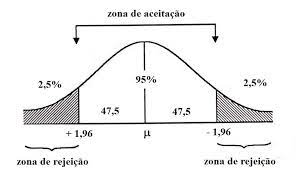 .
.
Já em testes unicaudais, o teste de hipótese é sempre se uma amostra é maior ou menor que outra:
Teste de cauda inferior:
H0: μ1 >= μ2
H1: μ1 < μ2
Teste de cauda superior
H0: μ1 <= μ2
H1: μ1 > μ2
O que define qual será é a cauda que será testada, a inferior ou a superior.
Nesse caso, a árera de rejeição se concentra em uma das caudas:
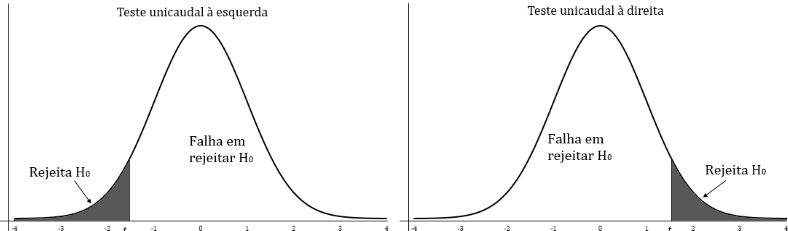
Vou deixar uma imagem que faz o resumo disso tudo que eu comentei:
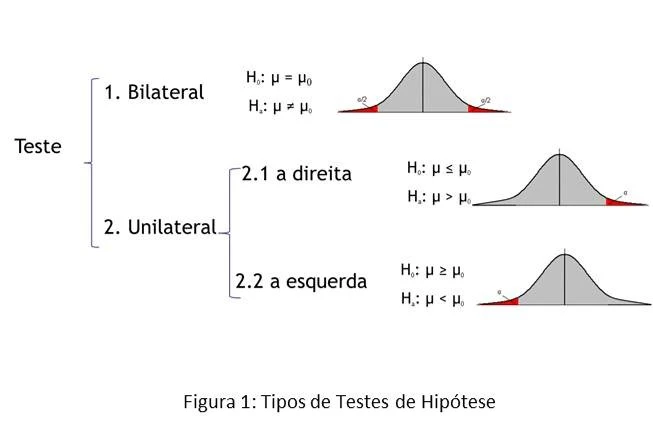
Agora vamos voltar para a função mannwhitneyu.
O parâmetrro alternative é o que define qual tipo de teste será usado na função:
As opções são:
Two-sided, para testes bilaterais;
less, para testes unicaudais à esquerda;
greater, para testes unicaudais à direita.
Caso este post tenha lhe ajudado, por favor, marcar como solucionado ✓.Bons Estudos!





 .
.
