Olá, Bruno, tudo bem?
Na tabela de distribuição normal, buscamos o valor de Z através dos valores da probabilidade de nossa curva.
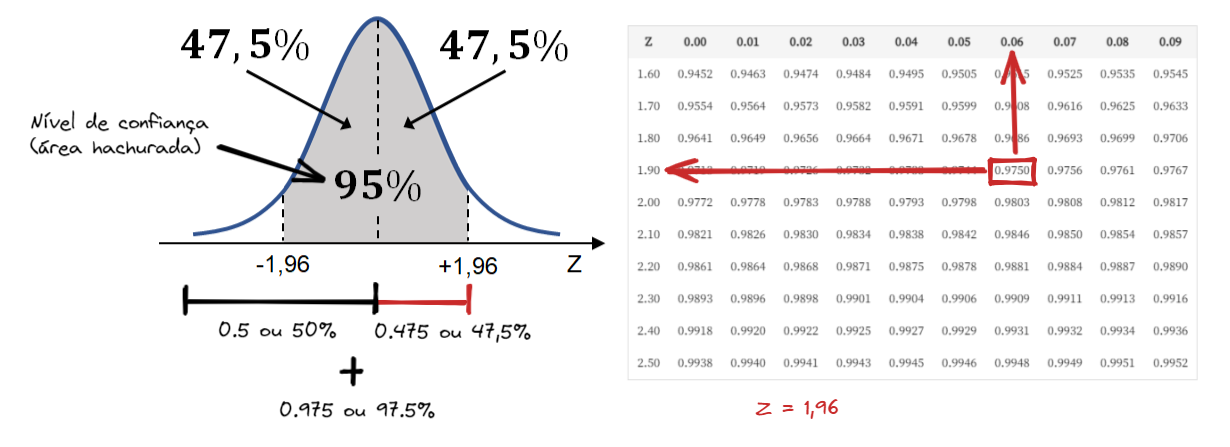
Para obtermos o z, temos que lembrar que ele é calculado pegando toda área abaixo dele. A região que está hachurada, no exemplo do professor, apenas demonstra onde está o nosso nível de confiança (de 95%).
Ou seja, para calular o z, pegamos o pico médio da curva para trás, que sabemos que vale 0.5, pois é o ponto que divide 50% da nossa distribuição em duas partes iguais espelhadas. E, além disso, somamos o intervalo entre o meio até a posição do z positivo.
Como temos uma função simétrica e sabemos que a área sob a curva de um z a outro é de 0.95, deveremos dividir por 2. Assim, saberemos que do meio da curva até o z positivo o valor será de 0.475 ou 47.5%.
Somando as duas áreas teremos 0.5 + 0.475 = 0.975.
Assim, para descobrirmos o valor de Z, basta procurar na nossa Tabela Normal Padronizada qual valor da área correspondente. Para 0.975 → z = 1,96.
Logo, para esse tipo de cálculo, contaremos do z positivo até o início, inclusive com o vazio anterior ao z negativo.
Espero ter ajudado e qualquer dúvida é só chamar!
Forte abraço!
Caso este post tenha lhe ajudado, por favor, marcar como solucionado ✓.Bons Estudos!





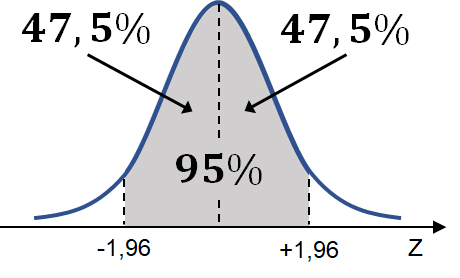 Pois é necessário para descobrir a extremidade que determina qual é o Z, e descobrindo a primeira extremidade, que pode ser 1,96, por exemplo, a outra já está pronta, que é a feita com a parte negativa: - 1,96.
Pois é necessário para descobrir a extremidade que determina qual é o Z, e descobrindo a primeira extremidade, que pode ser 1,96, por exemplo, a outra já está pronta, que é a feita com a parte negativa: - 1,96.