Em um cenário mais comum (ou "real"), não teremos previamente a média e desvio padrão da população para a variável aleatória estudada. O que fazer nesse cenário? Pelo que li a respeito, poderíamos usar a técnica de bootstrapping no lugar.
Você está vendo a versão anterior da nova experiência da Alura que estamos preparando para você. Em breve, ela ganha uma identidade visual novinha totalmente pensada em potencializar seus estudos!
Em um cenário mais comum (ou "real"), não teremos previamente a média e desvio padrão da população para a variável aleatória estudada. O que fazer nesse cenário? Pelo que li a respeito, poderíamos usar a técnica de bootstrapping no lugar.
Olá, Keroly! Tudo bem? Espero que sim.
Desculpe-nos pela demora em responder a sua dúvida.
Normalmente, quando não conhecemos a média e desvio padrão de uma população, existem duas formas mais comuns de contornar esse problema:
A técnica de bootstrapring aproxima-se dessa primeira. Nela, a partir de uma amostra, são criadas muitas amostras menores aleatorias. A partir dessas amostras, é tirada a média e desvio padrão de cada uma delas, e depois uma média de todas as médias e desvios padrão é adotada como estatísticas da população.
Como um exemplo dessa abordagem, trazemos logo abaixo uma aplicação prática de Bootstraping de notas de alunos geradas aleatoriamente e como fazemos todo o processo até o cálculo da média e desvio padrão usando essa técnica.
# Importando as bibliotecas
import random
import statistics
import numpy as np
import seaborn as sns
from scipy import stats
# Criando uma lista de notas aleatórias, o random.seed(101) mantém
# os mesmos valores aleatórios do nosso teste, caso queira reproduzi-lo
random.seed(101)
notas = [random.randint(5,10) for i in range(0,30)]
print(notas)Saída:
[9, 6, 9, 7, 8, 5, 10, 9, 6, 9, 6, 7, 8, 10, 6, 7, 8, 5, 7, 6, 6, 5, 8, 9, 7, 6, 8, 7, 6, 10]
Essa lista aleatória passa por uma reamostragem dentro da função meu_bootstrap(). Usamos um laço for para as reamostragens desejadas. A cada reamostragem, calculamos a sua média e preenchemos uma lista das médias das notas onde, nesse exemplo, consideramos o número de observações de 1000. Logo em sequência, plotamos o histograma dessa média estatística.
# Criando uma função para reamostragem
random.seed(101)
def meu_bootstrap(amostra):
reamostragem = random.choices(amostra, k = len(amostra))
media = statistics.mean(reamostragem)
return media
# Iterando a função e colocando na lista de médias
lista_de_medias = []
for i in range(1000):
x = meu_bootstrap(notas)
lista_de_medias.append(x)
# Plotando o histograma da lista das médias
ax = sns.histplot(data=lista_de_medias)Saída:
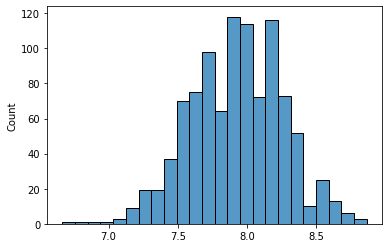
Como podemos observar, agora nossas amostras apresentam um comportamento de uma distribuição normal. E, sendo asim, podemos apresentar a estatística descritiva da seguinte forma:
# Estatística Descritiva da lista das médias
stats.describe(lista_de_medias)Saída:
DescribeResult(nobs=1000, minmax=(6.666666666666667, 8.866666666666667), mean=7.923766666666666, variance=0.10966592258925591, skewness=-0.13378866481793125, kurtosis=0.017562523199342372)
Por fim, para calcular a média e desvio padrão, utilizamos os dados provenientes da estatística descritiva acima da seguinte maneira:
# Imprimindo a media (arredondada em duas casas decimais)
# e o desvio padrão da reamostragem (arredondado em cinco casas decimais)
media_reamostragem = stats.describe(lista_de_medias)[2].round(2)
variancia_reamostragem = stats.describe(lista_de_medias)[3]
desvio_padrao_reamostragem = np.sqrt(variancia_reamostragem).round(5)
print(f"A média da reamostragem é {media_reamostragem} \nE o desvio padrão da reamostragem é {desvio_padrao_reamostragem}")
Esperamos que essa abordagem possa ter te ajudado a compreender um pouco mais o assunto e qualquer dúvida é só utilizar o fórum para que possamos trazê-la a melhor experiência no seu aprendizado aqui na Alura!
Abraços e bons estudos!