function verificaColisaoRaquete(){ if (xBolinha - raio < xRaquete + comprimentoRaquete && yBolinha - raio < yRaquete + alturaRaquete && yBolinha + raio > yRaquete) { velocidadeXBolinha *= -1; }
Essa última verificação, onde yBolinha + raio > yRaquete, não ficou clara p mim. Se o yBolinha + raio for maior que o yRaquete, não vejo aí uma colisão, mas sim, a passagem para toque nas bordas. Por favor, alguém me dá uma luz, com relação a isso. Deixo meu agradecimento.
Oi, Tiago! Tudo bem?
Para compreender a lógica por trás do comando inicialmente precisamos entender como se comporta o plano cartesiano do p5: com o x e o y crescendo no sentido positivo, ou seja, comporta-se visualmente não como o quadrante 4 do plano cartesiano tradicional, mas como um quadrante 1 invertido (de cabeça pra baixo).
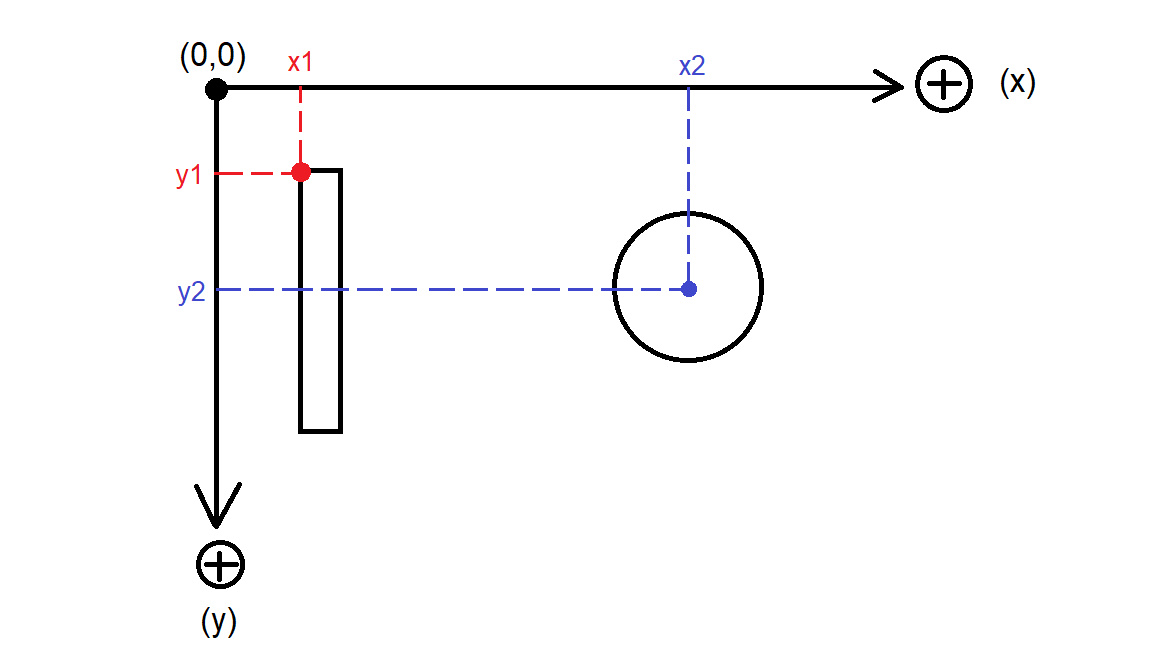
Somado a isso também devemos visualizar onde está o ponto que define a localização x e y da bolinha e da raquete (xRaquete = x1, xBolinha = x2, yRaquete = y1, yBolinha =y2), representados pelo ponto azul (para a bolinha) e pelo ponto vermelho (para a raquete) na imagem abaixo:
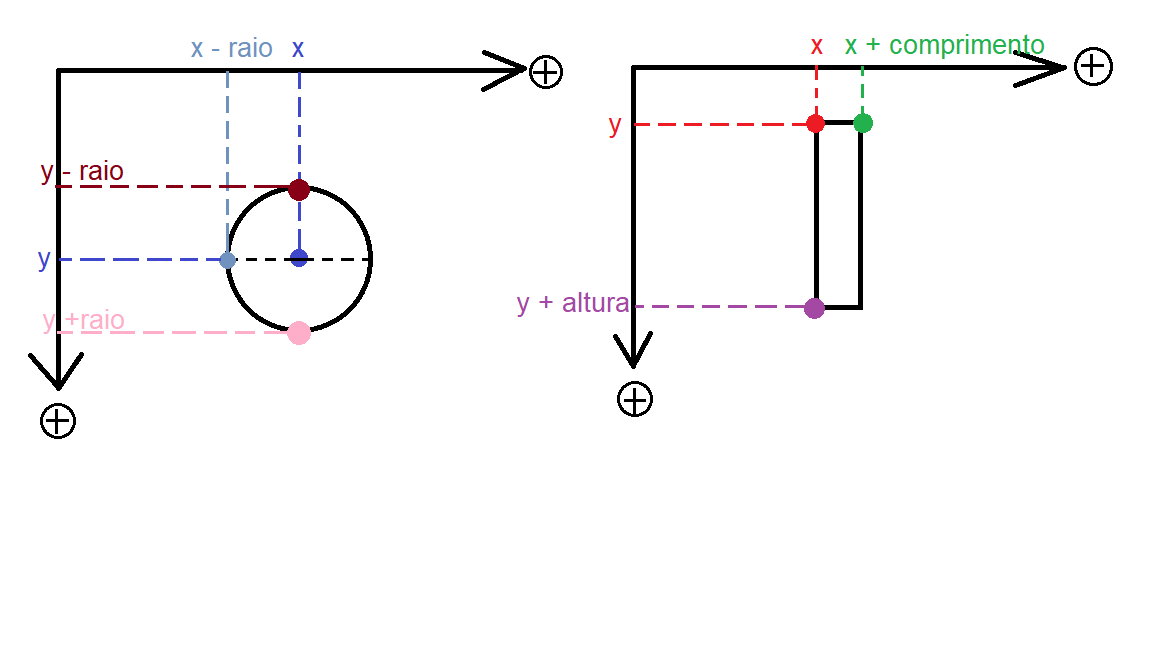
Além disso, é necessário visualizar a posição de cada comando, como xBolinha (bolinha azul), xBolinha - raio (bolinha cinza), yBolinha (bolinha azul), yBolinha + raio (bolinha rosa), yBolinha - raio (bolinha marrom),yRaquete + altura (bolinha roxa), xRaquete e yRaquete (bolinha vermelha) e xRaquete + comprimento (bolinha verde).
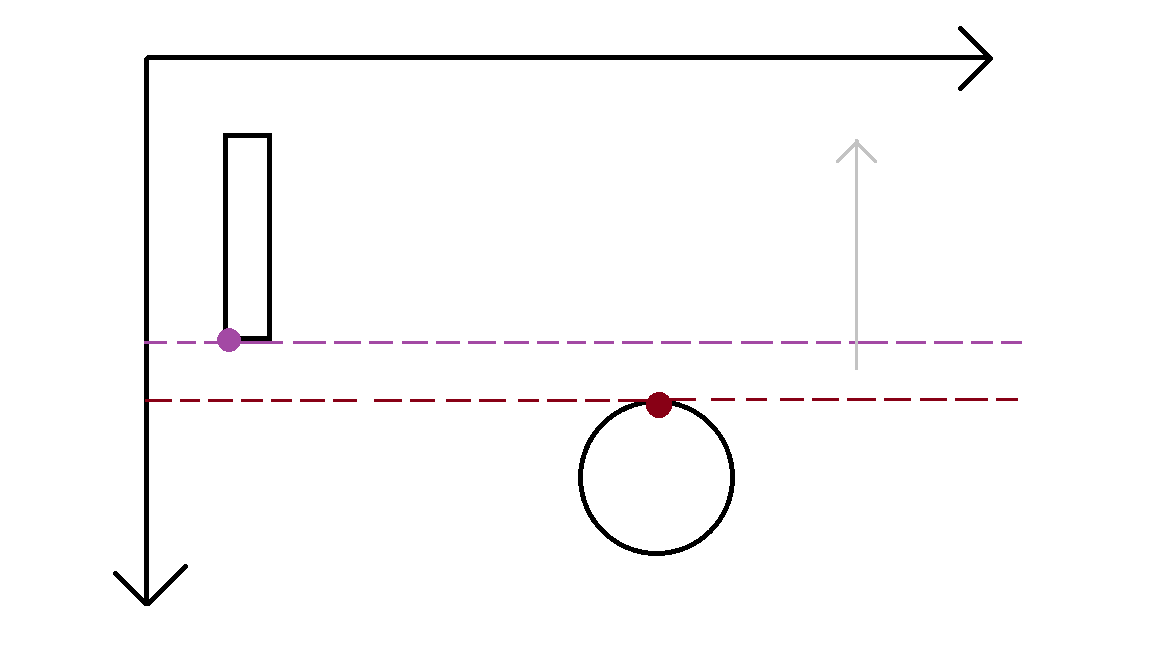
Dessa forma, podemos visualizar yBolinha - raio (ponto marrom) < yRaquete + alturaRaquete (ponto roxo), quando a linha marrom estiver localizada em uma região do eixo y menor que a localização da linha roxa, seguindo a movimentação da seta cinza, como podemos ver na imagem abaixo:
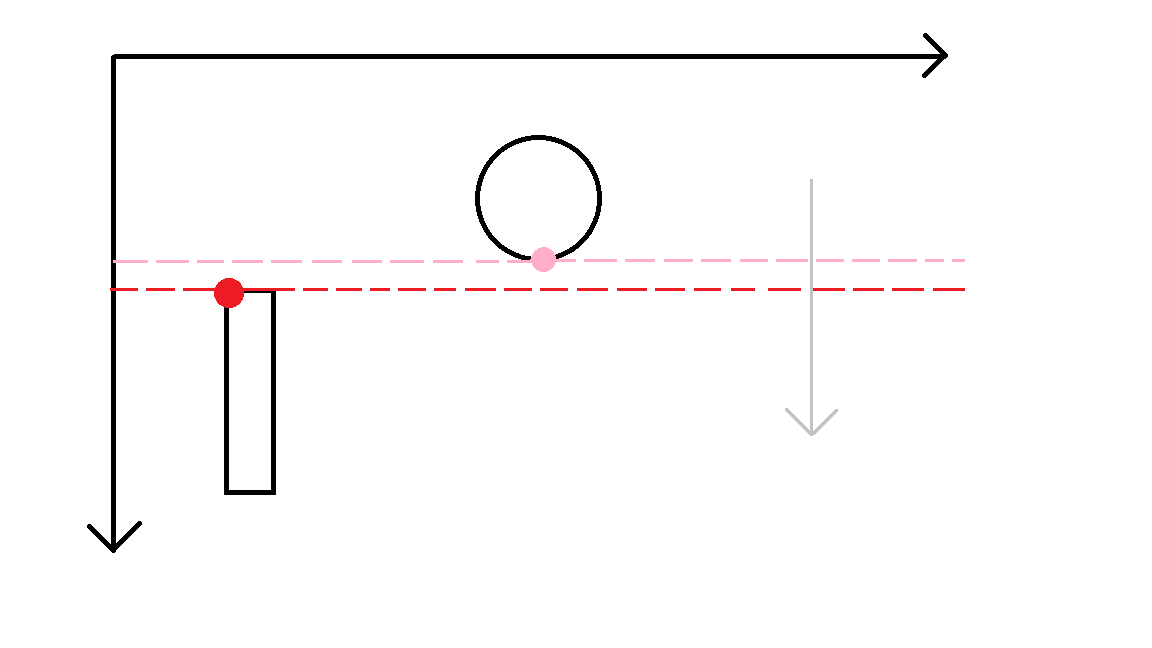
Enquanto isso, yBolinha + raio > yRaquete, corresponde a quando a localização no eixo y do ponto rosa (representada pela linha rosa) for maior que a localização no eixo y da bolinha vermelha (representada pela linha vermelha), seguindo o sentido da seta cinza.
Assim, limitamos a posição das extremidades da bolinha em relação às extremidades da raquete.
Espero ter ajudado! Qualquer dúvida é só comunicar!
Forte abraço e bons estudos!