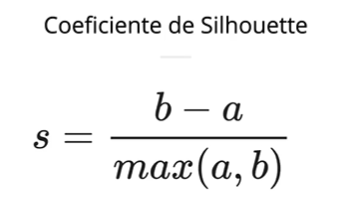Não consegui acompanhar a explicação matemática. Sou cego e as fórmulas matemáticas estão em forma de imagem na transcrição do vídeo, impossibilitando minha leitura. Também no vídeo, a linguagem é pouco descritiva. Poderiam me ajudar? Gosto sobremaneira de exatas, mas tenho essa dificuldade quanto a material e didáticas inclusivas.Obrigado!
hoje, com a Alura e o Google Gemini
Boa noite Pietro, tudo bem com você?
Peço desculpas pelo ocorrido, já solicitamos para o time de Transcrição dar uma atenção para a descrição das imagens desse curso. Para não impactar a continuidade dos seus estudos, trouxe a baixo uma transcrição prévia da atividade Matemática do Silhouette com a descrição das imagens.
Início da transcrição.
Temos a fórmula para calcular o coeficiente que se baseia em dois principais valores: beta e alfa.
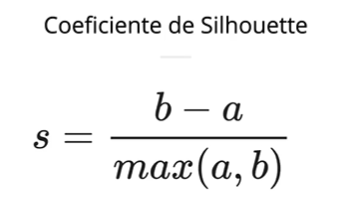
Começaremos por calcular o valor de alfa, isto é, a distância média entre o ponto e todos os outros pontos do mesmo cluster. Vamos verificar a compactação dos elementos.
Utilizaremos o mesmo exemplo dos três clusters, e cada um contém três elementos.
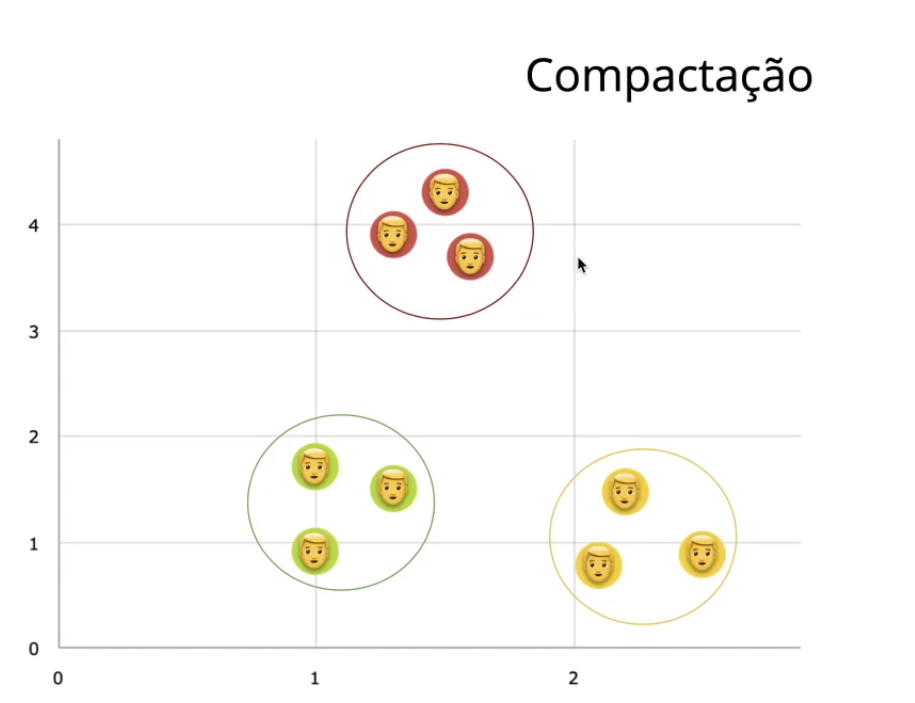
Nos basearemos em duas dimensões(x,y), e utilizaremos dois atributos dos 16 que temos disponíveis em nosso dataframe.
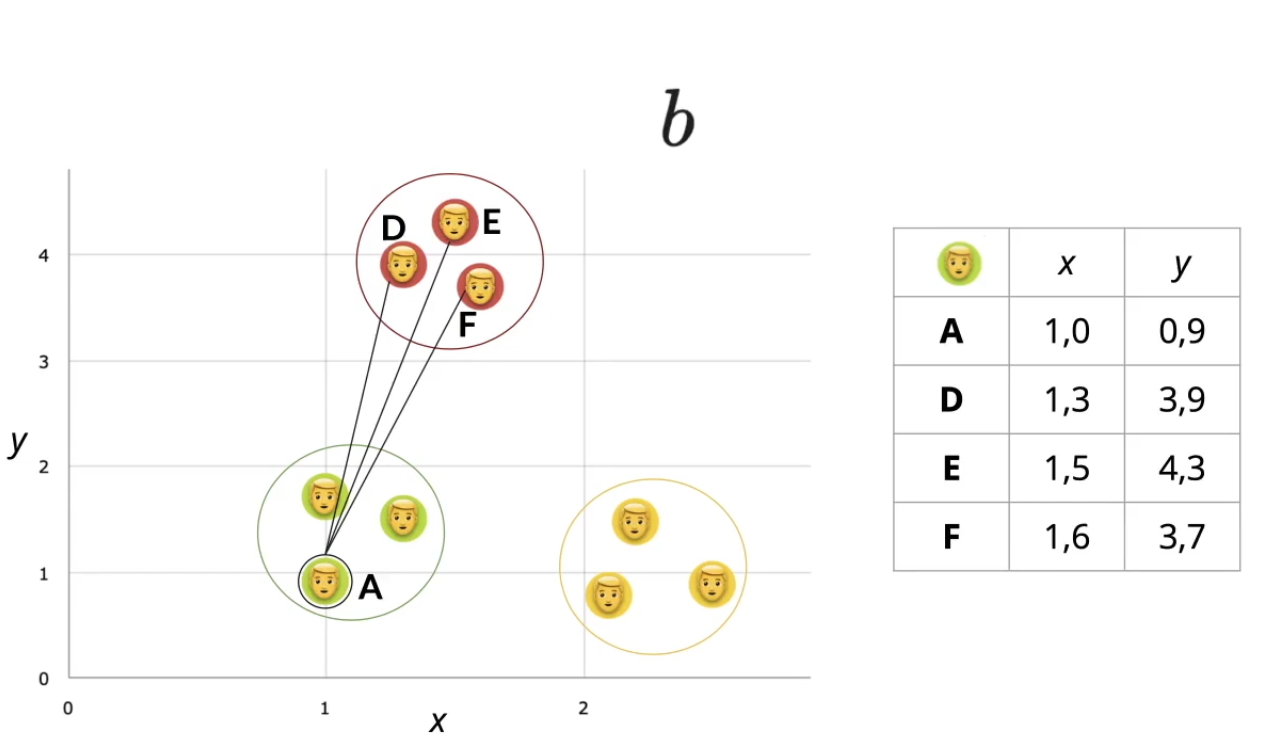
Selecionaremos um ponto específico, um cliente, e a partir dele calcularemos a média para outros elementos do cluster. Chamaremos este primeiro ponto de "A".
Para o eixo x utilizaremos o valor de 1,0 e para y 0,9. Feito isso, mediremos a distância do ponto "A" para o ponto "B" e "C"
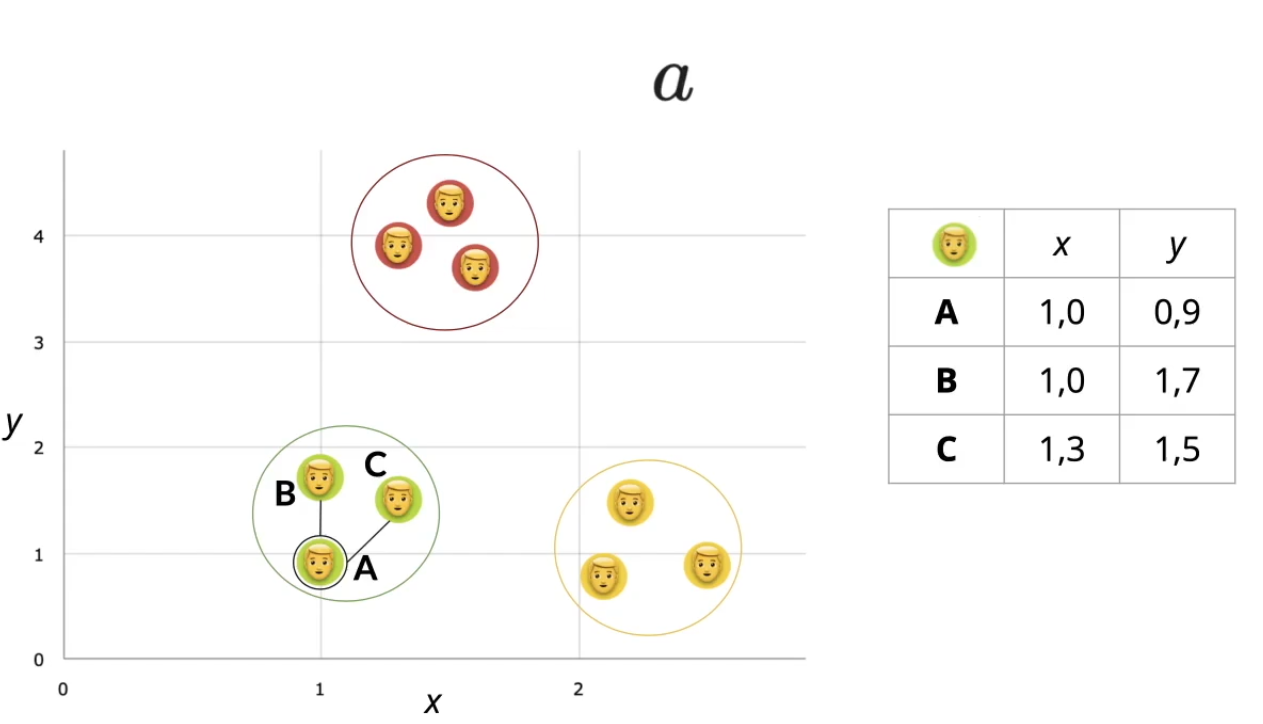
Estamos utilizando a distância euclidiana, portanto usaremos sua fórmula.
Pausa na transcrição.
Pietro, vou dividir em duas respostas porque existe uma limitação de caracteres nos posts.
Continuação da transcrição.
O resultado dos cálculo será de, 0,8. Essa é a distância Euclidiana entre A e B. Faremos o mesmo procedimento para C. A distância entre o ponto A e C é 1,12.
Feito isso, obteremos a média entre os dois valores finais, o resultado é 0,96. Voltaremos a fórmula do coeficiente de silhoette que apresentamos no início da aula e inseriremos esse valor na variável alfa.
Nosso próximo passo é calcular o valor de beta, que é a distância média entre o ponto e todos os outros pontos do cluster mais próximo.
Para sabermos qual é o cluster mais próximo, deveremos tirar a média entre os pontos para os dois clusters e coletar o menor valor. Faremos o mesmo procedimento que realizamos anteriormente, mas com pontos diferentes.
chegaremos ao resultado final de 3,1 do ponto A dos pontos do cluster vermelho. Para o cluster amarelo o resultado será de 1,31. A menor distância é o segundo cluster, como podemos verificar.
O resultado final será de 0,26. O resultado sempre está entre 1 e -1, então neste caso temos um bom valor positivo.
Fim da transcrição.
Espero ter ajudado, mas qualquer coisa é só mandar mensagem viu?!
Abraço e bons estudos.