Olá, boa tarde, gostaria de verificar se meu exercício está correto. Segue a resolução.

diametro_laranja = citrus[:5000,0] peso_laranja = citrus[:5000,1]

X = diametro_laranja Y = peso_laranja n = np.size(X)

(nnp.sum(XY) - np.sum(X)* np.sum(Y)) / (n*np.sum(X**2) - np.sum(X)**2)

#coloquei a1 para diferenciar das toranjas, que são o a2

a1 = (nnp.sum(XY) - np.sum(X)* np.sum(Y)) / (n*np.sum(X**2) - np.sum(X)**2)

np.mean(Y) - a1*np.mean(X)

b1 = np.mean(Y) - a1*np.mean(X)

y1=a1*X+b1

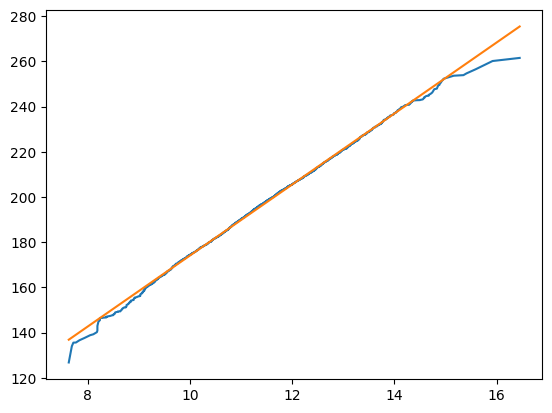
plt.plot(diametro_laranja, peso_laranja) plt.plot(X,y1) np.linalg.norm(X-y1)

#o gráfico ficou dessa forma:

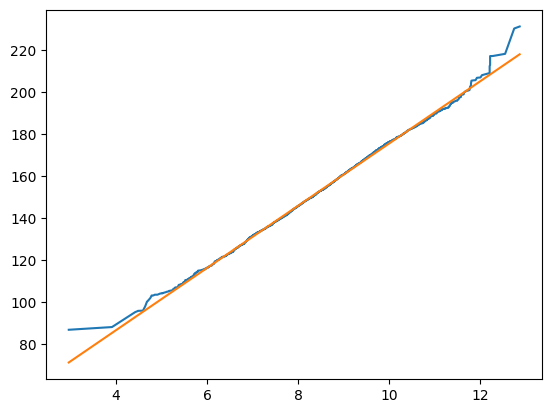
Análise das toranjas

diametro_toranja = citrus[5000:,0] peso_toranja = citrus[5000:,1]

W = diametro_toranja Z = peso_toranja n = np.size(W)

(nnp.sum(WZ) - np.sum(W)* np.sum(Z)) / (n*np.sum(W**2) - np.sum(W)**2)

a2 = (nnp.sum(WZ) - np.sum(W)* np.sum(Z)) / (n*np.sum(W**2) - np.sum(W)**2)

np.mean(Z) - a2*np.mean(W)

b2 = np.mean(Z) - a2*np.mean(W)

y2=a2*W+b2

plt.plot(diametro_toranja, peso_toranja) plt.plot(W,y2) np.linalg.norm(W-y2)