Como forma de fixar o conhecimento, vou escrever a solução com minhas palavras.
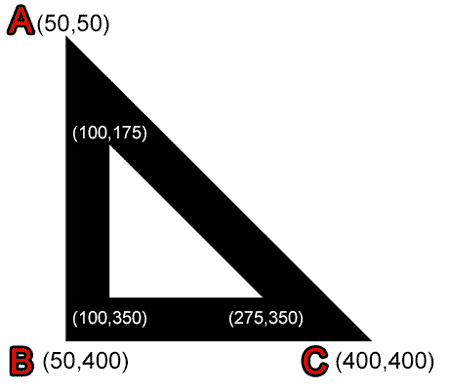
O exemplo pede para montar uma função que desenhe o triângulo preto e o triângulo branco. Sendo que devemos utilizar apenas os pontos A e C para realizar essa tarefa e que o triângulo branco deve ser sempre 2x menor que o triângulo preto.
function desenhaEsquadro(xa, ya, xc, yc, cor) {
pincel.fillStyle = cor
pincel.beginPath();
pincel.moveTo(xa, ya);
pincel.lineTo(xa, yc);
pincel.lineTo(xc, yc);
pincel.fill();
}A primeira parte do código é tranquila (construção do triângulo preto) pois é apenas no uso das coordenadas em A e C
Já para desenhar o triângulo branco é preciso levar 2 coisas em questão:
- As medidas de AB (largura e altura);
- As distâncias entre os pontos do triângulo preto e o dos pontos do triângulo branco.
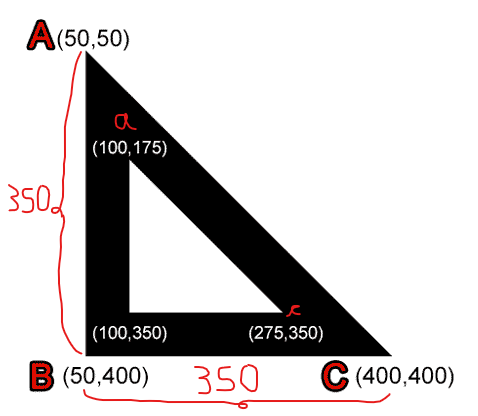
Encontrando os valores em xa:
Largura AC:
L = XC - XA = 400 - 50 = 350
Distância do ponto xa para XA:
xa - XA = 100 - 50 = 50
Encontrando a relação entre a distância do ponto xa para XA e a largura AC:
R = (xa - XA) / (XC - XA) = 50/350 = 1/7
Assim, ao encontrar a relação entre a distância do ponto xa para XA e a largura AC podemos agora generalizar para qualquer outra medida de triângulo preto que resultará em um ponto triângulo branco com a mesma relação encontrada (1/7).
xa = XA + ((XC - XA) / R) = XA + ((XC - XA) / 7) = (7XA + (XC - XA)) / 7 = (6XA + XC ) / 7
xa = (6XA + XC ) / 7
Encontrando os valores em xc:
Largura AC:
L = XC - XA = 400 - 50 = 350
Distância do ponto xc para XC:
xc - XC = 275 - 400 = -125
Encontrando a relação entre a distância do ponto xc para XC e a largura AC:
R = (xc - XC) / (XC - XA) = -125/350 = -5/14
Assim, ao encontrar a relação entre a distância do ponto xc para XC e a largura AC podemos agora generalizar para qualquer outra medida de triângulo preto que resultará em um ponto triângulo branco com a mesma relação encontrada (-5/14).
xc = XC + ((XC - XA) / R) = XC + (-5(XC - XA) / 14) = (14XC + (-5XC + 5XA)) / 14
xc = (9XC + 5XA ) / 14
Encontrando os valores em ya:
Altura AC:
A = YC - YA = 400 - 50 = 350
Distância do ponto ya para YA:
ya - YA = 175 - 50 = 125
Encontrando a relação entre a distância do ponto ya para YA e a altura AC:
R = (ya - YA) / (YC - YA) = 125/350 = 5/14
Assim, ao encontrar a relação entre a distância do ponto ya para YA e a altura AC podemos agora generalizar para qualquer outra medida de triângulo preto que resultará em um ponto triângulo branco com a mesma relação encontrada (5/14).
ya = YA + ((YC - YA) / R) = YA + (5(YC - YA) / 14) = (14YA + (5YC - 5YA)) / 14 = (9YA + 5YC ) / 14 ya = (9YA + 5YC ) / 14
Encontrando os valores em yc:
Altura AC:
A = YC - YA = 400 - 50 = 350
Distância do ponto yc para YC:
yc - YC = 350 - 400 = -50
Encontrando a relação entre a distância do ponto yc para YC e a altura AC:
R = (yc - YC) / (YC - YA) = -50/350 = -1/7
Assim, ao encontrar a relação entre a distância do ponto yc para YC e a altura AC podemos agora generalizar para qualquer outra medida de triângulo preto que resultará em um ponto triângulo branco com a mesma relação encontrada (-1/7).
yc = YC + ((YC - YA) / R) = YC + (-1(YC - YA) / 7) = (7YC + (-YC + YA)) / 7 = (6YC + YA) / 7
yc = (6YC + YA) / 7
Assim, por fim, temos o código completo. Lembrando que o ponto b é dado por (xa,yc).
function desenhaEsquadro(xa, ya, xc, yc, cor) {
pincel.fillStyle = cor
pincel.beginPath();
pincel.moveTo(xa, ya);
pincel.lineTo(xa, yc);
pincel.lineTo(xc, yc);
pincel.fill();
pincel.fillStyle = 'white'
pincel.beginPath();
pincel.moveTo((6*xa + xc)/7, (9*ya + 5*yc)/14);
pincel.lineTo((6*xa + xc)/7, (ya + 6*yc)/7);
pincel.lineTo((5*xa + 9*xc)/14, (ya + 6*yc)/7);
pincel.fill();
}

