Olá professor, acabei não entendendo o conceito por trás de pegar o menor valor gerado. A ideia seria escolher a menor diferença entre Moscow e o eixo y para ficar próximo da reta de regressão linear?
Aqui no meu notebook, a variável norma 2 saiu com os seguintes valores:
array([108.78167573, 196.42381103, 215.90315033, 113.53021234, 115.01273776, 131.86193375, 108.68115751, 160.95398594, 182.97491752, 143.95429885, 180.00431816, 101.79975701, 145.94291982, 144.96446943, 216.10415194, 170.66187046, 209.32945593, 172.01174311, 159.44027968, 101.93967982, 239.47661678, 180.28114121, 103.24349363, 111.67696159, 163.88537665, 138.45620335, 153.83599111, 102.910187 , 197.0563282 , 102.37165309, 165.10504814, 174.44160448, 101.80157959, 163.7920983 , 134.84976427, 106.11981797, 168.2354798 , 110.15005384, 103.48933025, 162.23742531, 102.10899613, 108.62067974, 106.98013659, 149.09907412, 122.53837358, 141.79870816, 104.87111375, 153.13981429, 152.24736686, 160.59683808, 141.82792488, 104.05242928, 160.82860535, 114.78004636, 122.76887943, 132.4811833 , 134.41433745, 104.00568461, 184.83118937, 198.32439767, 129.44816109, 108.88586429, 212.51401241, 122.37667657, 232.06924682, 153.77298102, 103.61094281, 110.96483795, 109.43902399, 166.82477566, 207.08161661, 208.30414437, 136.73400671, 220.58278532, 186.10473401, 121.77641615, 131.23361895, 154.86235999, 136.82776979, 179.39065105, 204.0699072 , 221.15846621, 130.16391043, 229.6621366 , 207.94622805, 103.56839473, 130.51959508, 142.93113145, 102.81836226, 111.94795706, 127.85654375, 134.25560339, 120.92074686, 188.19762043, 166.49005908, 117.65599445, 160.76099868, 111.55411516, 125.98776461, 120.65668015])
Dessa forma, o resultado do coeficiente angular ficou bem discrepante do original:
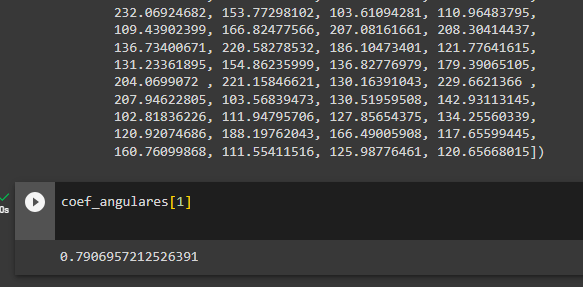
Acabei fazendo uma varredura visual procurando uma posição menor e usei coef_angulares[11] pra chegar num valor mais próximo




