[Dúvida] Dúvida sobre o significado da função np.linalg.norm e sobre o uso do seu valor retornado

Espero que ajude ..

Ótima pergunta! A função np.linalg.norm do NumPy é usada para medir o "tamanho" ou a "distância" de algo. No contexto de vetores e matrizes, ela mede o quão grande ou distante algo está em relação à origem.

No seu caso, se você está analisando a aproximação de uma reta aos seus dados, o valor retornado pelo np.linalg.norm pode representar o "erro" ou a diferença entre os pontos reais e a reta ideal.

Agora, respondendo às suas dúvidas:

O que o valor de retorno significa? Ele mede a distância total entre os pontos reais e a reta estimada. Quanto menor for esse valor, mais próxima a reta está dos seus dados.

Ele é igual ao coeficiente de correlação (r) da regressão linear? Não. O coeficiente de correlação (r) mede o quão forte é a relação entre as variáveis, variando de -1 a 1. Já o np.linalg.norm mede a diferença absoluta entre os pontos e a reta. Eles são conceitos diferentes.

Existem limites mínimos e máximos? O mínimo seria zero, o que indicaria que todos os pontos caem exatamente sobre a reta (nenhum erro). Não há um limite máximo fixo porque depende da escala dos seus dados.

Como isso ajuda na análise? Se o valor for pequeno, significa que a reta representa bem os dados. Se for grande, significa que a reta não se ajusta bem, e pode ser necessário um modelo melhor.

Ele indica se os dados estão distribuídos em uma reta? Indiretamente, sim. Se o valor do np.linalg.norm for pequeno, significa que os pontos estão bem alinhados. Se for grande, os pontos estão mais dispersos.

Muito obrigada pelo retorno. A explicação ajudou a clarear bastante as minha dúvidas.

Mas ainda resta uma questão ...

Fiz o projeto das laranjas e toranjas como atividade do final deste módulo e surgiu uma dúvida sobre a interpretação dos valores das funções linalg.norm para as regressão das laranjas e das toranjas.

Os valores foram muito altos, acima de 10000, entretanto, as retas da regressão linear se ajustaram bem melhor do que no exemplo do array das maçãs e Moscow, que apresentou um valor muito inferior para a função linalg.norm (próximo).

Postei a dúvida no fórum. Agradeço se você conseguir dar uma olhada, para tirar só mais esta dúvida.

Obrigada.

Bom dia , teria como mandar o código para que eu possa ter uma perspectiva melhor .

Segue o código da regressão das laranjas:

import numpy as np # Importação da biblioteca NumPy

url = "https://raw.githubusercontent.com/Marina-Falcao-DEV/Dataset_Citrus_Alura_Numpy/refs/heads/main/citrus.csv"

dados_total_citrus = np.loadtxt(url, delimiter = ",", skiprows = 1, usecols = np.arange(1, 6, 1)) # Ajustes para criação do array com os valores (excluindo a primeira coluna e a primeira linha)
print(dados_total_citrus)

# Verificando as características do array completo:
print("-"*20, "CARACTERÍSTICAS DO ARRAY (COMPLETO)","-"*20)
print(f"\nEste é um dataset com {dados_total_citrus.ndim} dimensões.") # Verificando quantas dimensões tem o array
print(f"Este é um dataset com {dados_total_citrus.shape[0]} linhas e {dados_total_citrus.shape[1]} colunas.") # Verificando a quantidade e linhas e colunas do array
print(f"Este é um dataset com {dados_total_citrus.size} elementos.") # Verificando o número de itens do array
print("="*77)

# Filtrando as colunas de diâmetro [posição 0] e peso [posição 1] do array total e criação de arrays específicos para laranjas e toranjas:
diametro_laranja = dados_total_citrus[:5000, 0]
diametro_toranja = dados_total_citrus[5000: , 0]
peso_laranja = dados_total_citrus[ :5000, 1]
peso_toranja = dados_total_citrus[5000: , 1]


# Regressão linear das laranjas
print("-"*25, "REGRESSÃO LINEAR DAS LARANJAS", "-"*25)
xl = diametro_laranja
yl = peso_laranja
n1 = peso_laranja.size
print(f"N{chr(176)} de elementos no array laranjas: {n1}")

a1 = (n1*np.sum(xl*yl) - np.sum(xl)*np.sum(yl))/(n1*np.sum(xl**2)-np.sum(xl)**2) # Cálculo do coeficiente angular da reta das laranjas
print(f"Coeficiente angular da reta das laranjas: {a1:.2f}")
b1 = np.mean(yl) - a1*np.mean(xl) # Cálculo do coeficiente linear da reta das laranjas
print(f"Coeficiente linear da reta das laranjas: {b1:.2f}")

print(f"Função linalg.norm: {np.linalg.norm(diametro_laranja-yl):.2f}")
plt.plot(diametro_laranja, peso_laranja) # Exibição dos resultados das amostras
plt.plot(xl, xl*a1+b1) # Exibição da reta de regressão (estimativa do valor)
plt.plot(8.5, a1*8.5+b1, "Dr") # Estimativa do valor do eixo y considerando o eixo x com valor de 8.5
plt.plot(15, a1*15+b1, "Dr") # Estimativa de valor do eixo y considerando o eixo x com valor hipotético de 15
plt.legend(["Laranjas"])

print("-"*20, "GRÁFICO DE REGRESSÃO LINEAR DAS LARANJAS", "-"*20)

E a parte do código da regressão das toranjas:

# Regressão linear das toranjas
print("-"*25, "REGRESSÃO LINEAR DAS TORANJAS", "-"*25)
x2 = diametro_toranja
y2 = peso_toranja
n2 = peso_toranja.size
print(f"N{chr(176)} de elementos no array toranjas: {n2}")

a2 = (n2*np.sum(x2*y2) - np.sum(x2)*np.sum(y2))/(n2*np.sum(x2**2)-np.sum(x2)**2) # Cálculo do coeficiente angular da reta das toranjas
print(f"Coeficiente angular da reta das toranjas: {a2:.2f}")
b2 = np.mean(y2) - a2*np.mean(x2) # Cálculo do coeficiente linear da reta das toranjas
print(f"Coeficiente linear da reta das toranjas: {b2:.2f}")

print(f"Função linalg.norm: {np.linalg.norm(diametro_toranja-y2):.2f}")
plt.plot(diametro_toranja, peso_toranja) # Exibição dos resultados das amostras
plt.plot(x2, x2*a2+b2) # Exibição da reta de regressão (estimativa do valor)
plt.plot(6, a2*6+b2, "pc") # Estimativa do valor do eixo y considerando o eixo x com valor de 6
plt.plot(20, a2*20+b2, "pc") # Estimativa de valor do eixo y considerando o eixo x com valor hipotético de 20
plt.legend(["Toranjas"])

print("-"*20, "GRÁFICO DE REGRESSÃO LINEAR DAS TORANJAS", "-"*20)

Gráfico de regressão dos preços das maçãs em Moscow, que foi bem mais divergente entre o ajuste da reta de regressão e dos dados, mas o valor da função linalg.norm foi bem inferior (101.7969) .

Regressão das laranjas: função linalg.norm = 10279.67

Regressão das toranjas: função linalg.norm = 13200.74

Resumindo ...

Regressão de Moscou tem o valor da função linalg.norm bem menor do que as regressões das laranjas e toranjas, entretanto, o gráfico de Moscow está menos alinhado à reta de regressão em comparação aos gráficos das laranjas e toranjas. Como isso é possível?

No meu entendimento, o valor linalg.norm das laranjas e toranjas deveria ser menor do que o de Moscow, pois os dados delas estão mais alinhados com a reta de regressão.

Para explicar essa situação de forma simples e sem muitos termos técnicos, vou usar uma analogia e focar no conceito de "erro" ou "distância" entre os pontos e a reta de regressão.

Explicação simples:

O que é a reta de regressão?

A reta de regressão é uma linha que tenta "prever" ou "resumir" o comportamento dos dados. Ela é desenhada de forma a ficar o mais perto possível de todos os pontos no gráfico.

O que a função linalg.norm mede?

A função linalg.norm mede o "erro total" entre os pontos reais e a reta de regressão. Quanto menor esse valor, mais próximos os pontos estão da reta. É como se fosse uma medida de "quanto os pontos estão fora do lugar".

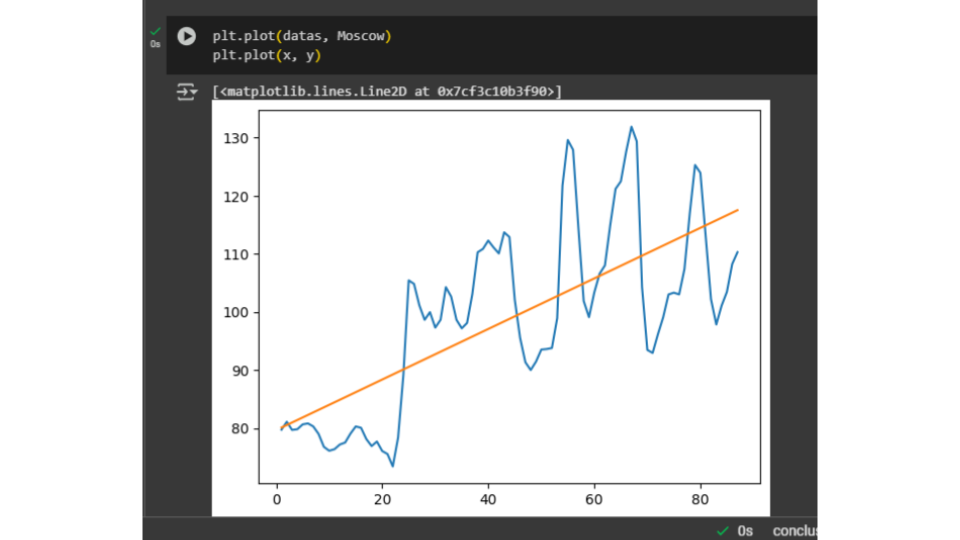
Por que o gráfico de Moscow tem um linalg.norm menor, mas parece menos alinhado?

Imagine que os preços das maçãs em Moscow variam muito (os pontos estão espalhados), mas a reta de regressão foi desenhada de forma que os erros (as distâncias dos pontos até a reta) são pequenos em média. Isso pode acontecer se os pontos estiverem relativamente próximos da reta, mas em grandes quantidades.

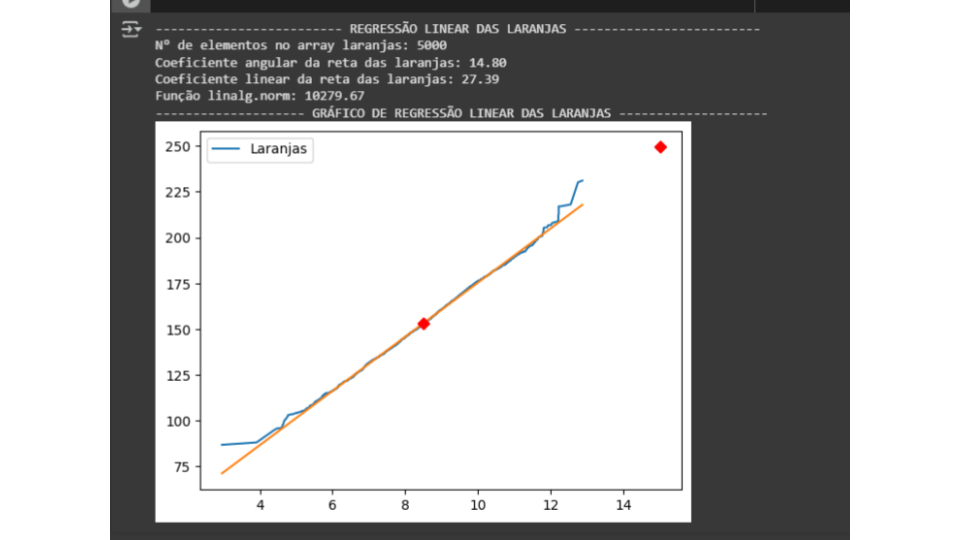
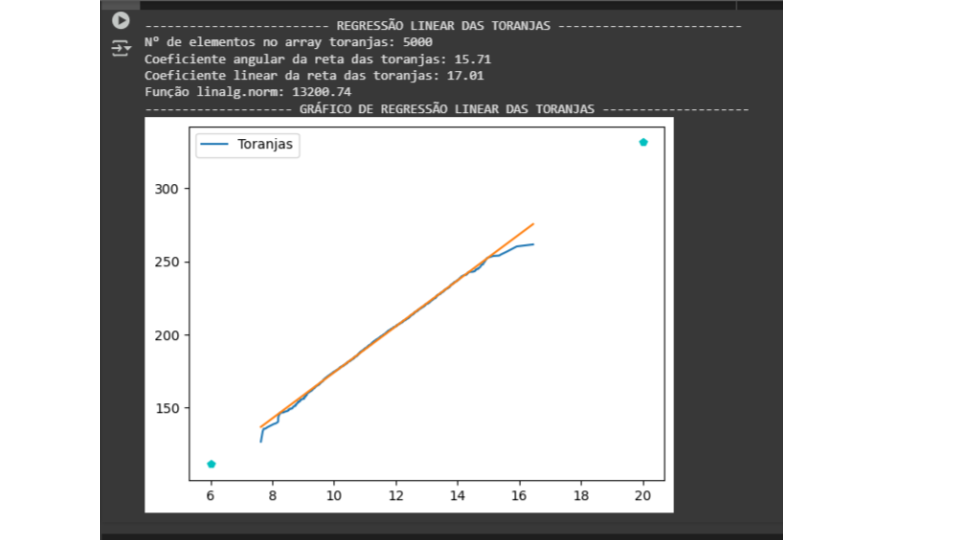
Já no caso das laranjas e toranjas, os pontos podem estar mais alinhados visualmente, mas alguns pontos estão muito longe da reta. Esses pontos "fora do padrão" aumentam muito o valor do linalg.norm, mesmo que a maioria dos pontos esteja bem alinhada.

Resumindo:

O linalg.norm mede o erro total, não apenas o alinhamento visual. No caso de Moscow, os erros são pequenos, mas os pontos estão mais espalhados. Já nas laranjas e toranjas, alguns pontos estão muito longe da reta, o que aumenta o erro total, mesmo que a maioria dos pontos esteja bem alinhada.

Analogia:

Pense em duas turmas de alunos:

Na turma de Moscow, todos os alunos tiraram notas parecidas (erros pequenos), mas essas notas variam bastante (pontos espalhados).

Na turma das laranjas e toranjas, a maioria dos alunos tirou notas muito parecidas (pontos alinhados), mas alguns alunos tiraram notas muito diferentes (pontos distantes), o que "estraga" a média.

O linalg.norm é como a soma de todas as diferenças das notas em relação à média. Na turma de Moscow, as diferenças são pequenas, mas há muitas. Nas outras turmas, as diferenças são grandes para alguns alunos, o que aumenta o valor total.

Espero que isso ajudado .

Resposta perfeita e muito esclarecedora. Agora entendi.

Muito obrigada pela explicação, exemplos comparativos e rapidez da resposta.

Disponha