Oi Paulo! Como você está?
Na primeira vez que verificamos a colisão com as bordas, estávamos delimitando o espaço em que a bolinha poderia se mover. Antes dessa função, a bolinha se moveria infinitamente em uma mesma direção, tendo seu x e y cada vez maiores. Por isso na função verificaColisaoBorda() os parâmetros utilizados são width e height, que são parâmetros embutidos no P5.JS e que dizem respeito ao tamanho que definimos na função setup() . Vamos relembrá-la:
function setup() {
createCanvas(600, 400);
Logo, width corresponde ao x da tela, e height ao y da tela.
function verificaColisaoBorda() {
if (xBolinha + raio > width || xBolinha - raio < 0) {
velocidadeXBolinha *= -1;
}
if (yBolinha + raio > height || yBolinha - raio < 0) {
velocidadeYBolinha *= -1;
}
}
Aqui, se a posição da bolinha for maior ou menor que o tamanho da tela, a velocidade será invertida: ao tocar na borda, a bolinha muda de direção.
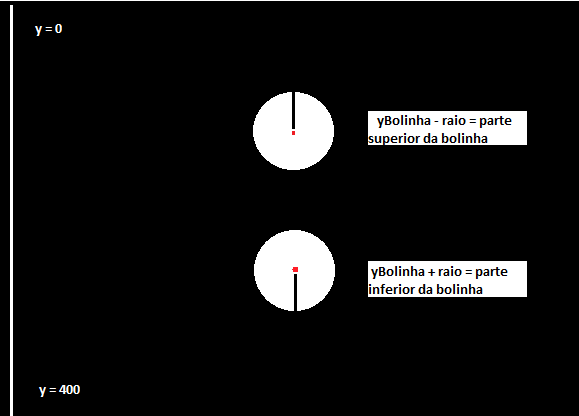
Quando criamos a função verificaColisaoRaquete(), a estratégia foi comparar a posição x da bolinha com a posição x da raquete, como está na primeira condição da função: xBolinha - raio < xRaquete + raqueteComprimento. Subtraímos o raio da bolinha para que ela seja considerada em sua totalidade, já que o x representa o ponto central do objeto, e o mesmo acontece com a adição do comprimento da raquete. Portanto, essa estratégia faz com que a bolinha reconheça todo o espaço equivalente ao tamanho da raquete, na borda esquerda da tela, e a colisão com a borda para de ocorrer.
Para isso entram as próximas duas verificações: yBolinha - raio < yRaquete + raqueteAltura && yBolinha + raio > yRaquete, que comparam a posição y (vertical) da bolinha e da raquete, e garantem que a bolinha apenas vai reconhecer a raquete quando o y dos dois objetos forem equivalentes.
Vou deixar aqui um artigo bem legal que fala sobre como funciona o plano cartesiano no P5.JS e que pode ajudar a compreender como funcionam esses cálculos condicionais:
Espero que tenha ficado mais claro, Paulo. Estou a disposição.
Caso este post tenha lhe ajudado, por favor, marcar como solucionado ✓. Bons Estudos!