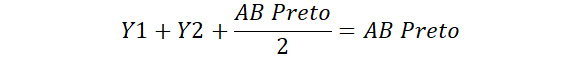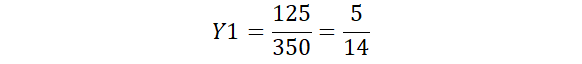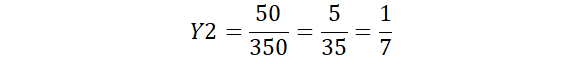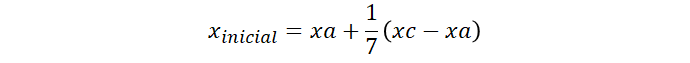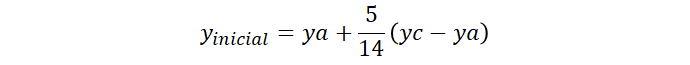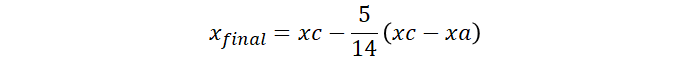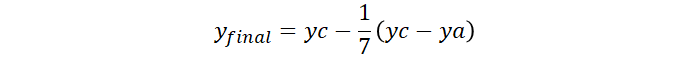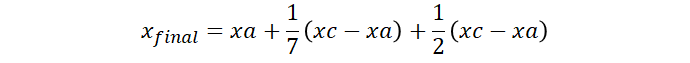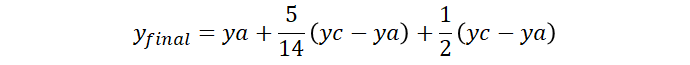Cálculo do triângulo interno

E ae Lucas, tudo tranquilo?

Vou tentar fazer uma explicação grande aqui... hhahahahahah

Qualquer dúvida só falar!

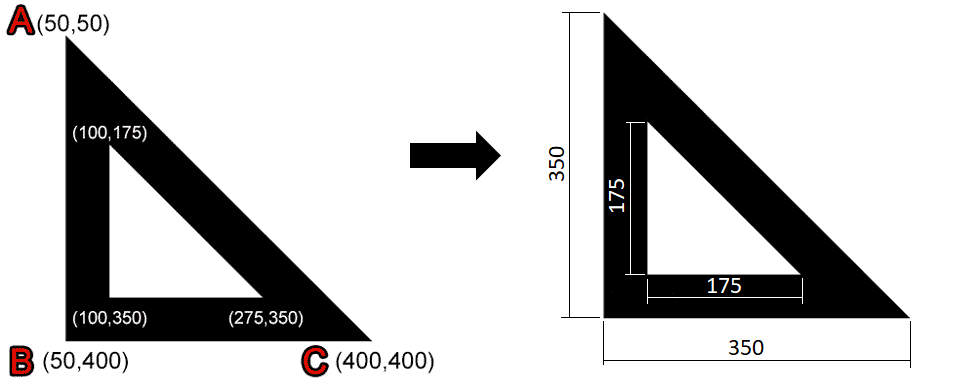
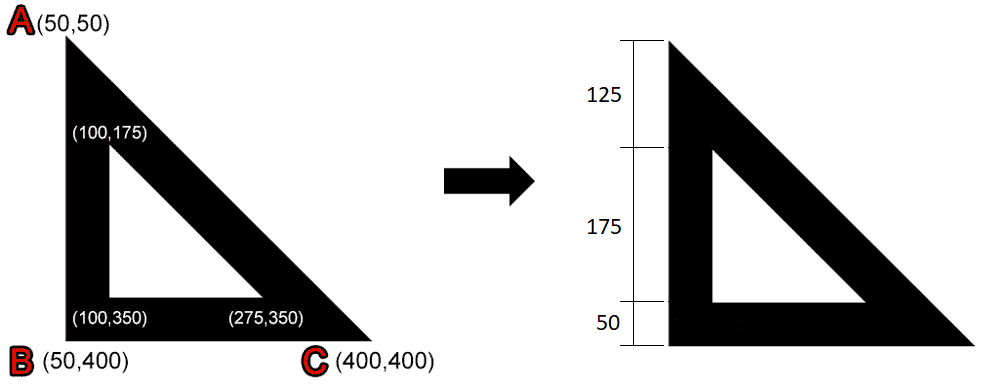
Da imagem principal com os pontos, podemos tirar as medidas dos triângulos conforme imagem abaixo:

• Triângulo preto: reta AB = B(50,400) - A(50,50) = (0,350)
• Triângulo branco: reta AB = B(100,350) - A(100,175) = (0,175)
• Como x = 0, o valor do comprimento da reta AB é igual ao de y. No caso triângulo preto é y = 350 e o triângulo branco y = 150
• Retas BC seguem o mesmo raciocinio da reta AB.

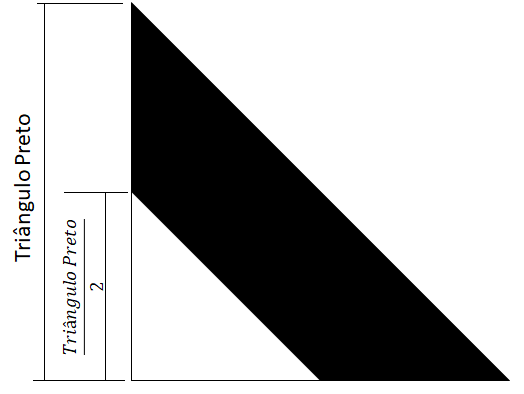
Com essas medidas dos catetos (350 no preto e 175 no branco), temos que os triângulos são semelhantes e pela razão da proporcionalidade;

• Triângulo branco é a metade do triângulo preto, 175 / 350 = 1/2

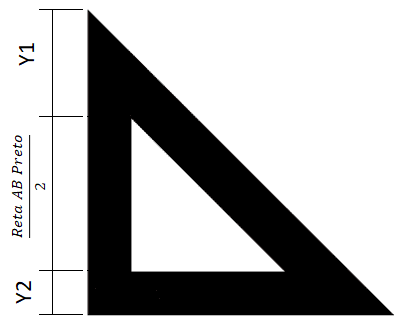
Sabendo a proporção do triângulo branco, fica mais claro encontrar as outras proporções de posicionamento:

• Se a reta AB do triângulo branco é a metade da reta AB do triângulo preto.
• Pela imagem abaixo temos que (Y1) + (Y2) é igual a outra metade da reta AB do triângulo preto.
• Com isso, a soma de todos os segmentos de retas que achamos vai ser o comprimento da reta AB do triângulo preto, 350.

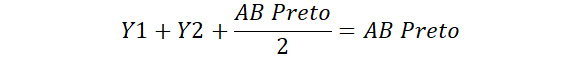
Agora é só achar as proporções restante.

Com as medidas da imagem principal achamos os seguintes valores:

• Y1 = 125;
• Y2 = 50;

Agora se 175 é a metade de 350. Quanto é os valores de 50 e 125? Só realizar os calculos e simplificar:

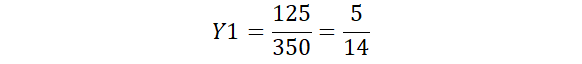
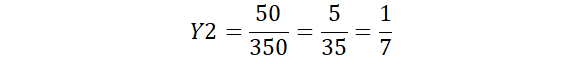
Agora temos todas as proporções do triângulo branco em relação ao triângulo preto:

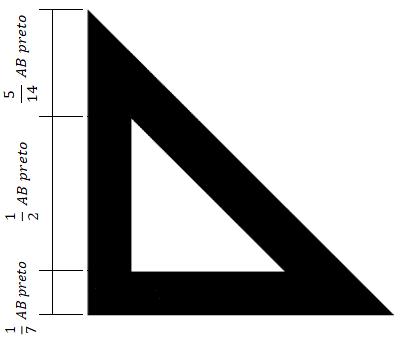
O mesmo pode ser feito com a reta BC:

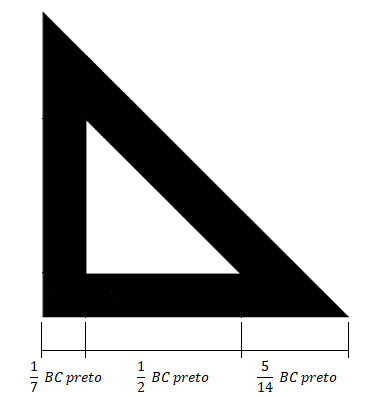
Sendo assim pode escrever o x inicial, y inicial, x final e y final do triângulo brancos:

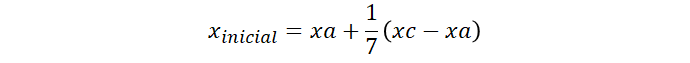
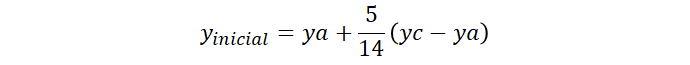
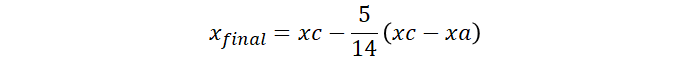
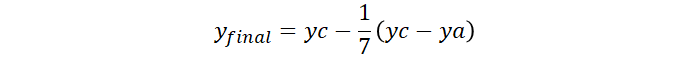
Com esses valores você pode encontrar o denominador comum e escrever como o professor fez.

O x final e y final também podem ser escrito como:

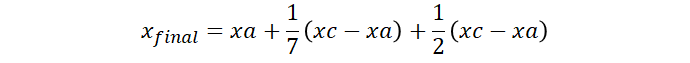
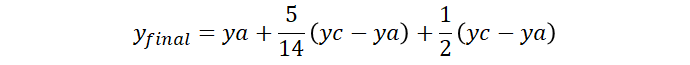
Assim o código pode ser escrito como:

function desenhaEsquadro(xa, ya, xc, yc, cor) {
        pincel.fillStyle = cor
        pincel.beginPath();
        pincel.moveTo(xa, ya);
        pincel.lineTo(xa, yc);
        pincel.lineTo(xc, yc);
        pincel.fill();

        xi = xa + (1/7)*(xc-xa)
        xf = xc - (5/14)*(xc-xa)
        yi = ya + (5/14)*(yc - ya)
        yf = yc - (1/7)*(yc - ya)
        pincel.fillStyle = 'white'
        pincel.beginPath();
        pincel.moveTo(xi, yi);
        pincel.lineTo(xi, yf);
        pincel.lineTo(xf, yf);
        pincel.fill();

    }

É isso!

Espero que tenha ajudado essa explicação.

Abraço!